【塾生必読】2019 第3回石川県総合模試を解いてみた

第3回石川県総合模試が実施されましたが、みなさんいかがだったでしょうか。毎回「数学が難しかった」という声をよく聞きますが、難問・奇問はほとんどありません。しっかりと復習をしてどこで詰まっていたのかをよく考えてみましょう!まだまだ焦る時期ではないので、1つ1つの問題を丁寧にやることが大切ですよ!
第2回の解いてみたを華麗にスルーしての第3回石川県総合模試を解いてみたです。
第2回は時期的に時間がほとんどなく「解いてみたどころじゃないぞ!」という状態でしたので、今回はちょっと頑張って記事を書きます(笑)
概観
大問7、小問22という石川県総合模試の標準的なセットでした。総合模試は大問が7〜8、小問が20〜25というセットが多いです。
ただし、時間的には非常に厳しいセットであり、じっくり考えていると「半分も解けないうちに終わってしまった!」という生徒も出てくるでしょう。ペースの問題については時間内にきちんと解ける方がもちろん良いのですが、スピードを追い求めすぎることで起こり得る別の問題もあるため、あまり気にしすぎない方が良いと考えます。現実的には7割程度手がついていれば学力的には十分であると思います。
内容的には、前半は規則性・関数・方程式といった計算中心の問題で、後半が作図・平面図形・空間図形といった幾何の問題が中心となってバランスよく出題されています。難問・奇問のような問題はなく、入試標準レベルの問題が揃っているため復習をしっかりとやっていけば力はつくはずです(ただし、単に解き直しをするという復習では意味がありません!)。
問題の難易度的には「標準」ですが、時間的なことも含めて「やや難」といった感じでしょうか。
全体的な難易度やや難
各問題の概要
大問1
内容 小問集合
難易度 易
基本的な計算を中心とする小問集合です。ここは全員が満点を狙っていくべきところです。案外間違いが多いのが(1)のエのような問題です。$\displaystyle \frac{a+2b}{4}$ などとなっている場合に、分子の $a+2b$ は $(a+2b)$ と1つの数のように扱うのが原則です。このカッコの存在を無視してしまう人が多いので要注意です。
また、計算ミスが多いという人は、闇雲に計算練習をするのではなく、自分の癖を知ることが大切です。計算ミスの場合、途中式を書きすぎてミスしてしまう人や、逆に書かずにミスしてしまう人がいます。それぞれに合わせて練習を工夫してみてください。
例えば、(1)のオなどの計算で
\begin{align*}
\sqrt{48}-\sqrt{6}\times \sqrt{2} &=\sqrt{48}-\sqrt{12}\\
&=4\sqrt{3}-2\sqrt{3}\\
&=2\sqrt{3}
\end{align*}
と計算する人もいれば
\begin{align*}
\sqrt{48}-\sqrt{6}\times \sqrt{2} &=\sqrt{48}-\sqrt{12}\\
&=2\sqrt{12}-\sqrt{12}\\
&=\sqrt{12}\\
&=2\sqrt{3}
\end{align*}
と計算する人もいるでしょう。どちらが良いというわけではありません。人によって計算のやり方に癖があるのです。自分の癖にこだわり過ぎてミスが生じるようであれば、違う方法を試してみることもオススメします。また、模範解答通りに解く必要はまったくありませんので、模範解答にこだわり過ぎるのも考えものです。(まさか模範解答を赤ペンで写してるひとなんていないと思いますが・・・)
いずれにしても、計算力がないのは致命的なのでここで点数が取れていない人は何よりもまず計算練習をきちんとやりましょう。
いつも言ってるけど中学生のうちに暗算力を鍛えておくといいぞ〜!
大問2
内容 規則性
難易度 易
規則性の問題というだけで解くのを諦めた人もいるかもしれません。が、実際には規則性が関係するのは(1)だけ(それもほぼ必要ないですが)で、(2)は単なる証明問題です。問題の見た目に惑わされないように注意しておきましょう。
(1)については、いちばん確実な方法は6行目まですべて書いてしまうことです。出てくるのは奇数だけなので、ただ奇数を順番どおりに書いて表を埋めてしまえば誰でも正解にたどり着きます。こうした方法を「数学的ではない」などと言ってバカにする人もいるようですが、具体例というのは非常に価値のあるものです。よい方法が思いつかないときに、すぐに具体的な数値で確かめてみたりすることができるかどうかはとても大切な能力です。
もう少しラクをしたい人は、縦に並ぶ数に着目して計算で求めることもできます。4列目の数は、上から7、19、31となり、12 ずつ増えています。したがって、4行目は $31+12=43$、5行目は $43+12=55$、6行目は $55+12=67$ となりますね。
(2)は連続する奇数において、各奇数の平方の差が8の倍数になることを証明する問題です。
問題では表が関連するかのうような見た目をしていますが、証明すべきことを確認するとこの表はとくに必要ないことが分かります。
連続する2つの奇数は、$2n+1$、$2n+3$ のように表すこともできますが、対称性を意識して $2n-1$、$2n+1$ と表す方が計算がラクになることが多いです。
ある偶数 $2n$ の両隣が連続する奇数であるという捉え方のほうが何となくスッキリしませんか?
連続する奇数を $2n-1$、$2n+1$ とおいたらあとは平方の差を計算するだけです。
$$(2n+1)^2-(2n-1)^2=8n$$
となり、8の倍数となることが分かります。
大問3(復習おすすめNo.1)
内容 関数
難易度 やや難
関数の問題ですが「よく意味がわからなかった」という生徒も少なからずいました。問題文が長いこと、グラフが2つ登場することを考慮すると受験生には少しとっつきにくい問題だったようです。問題文が長い場合に一気に全部読んでしまおうという人や、長くて読む気が失せるという人が出てきます。どちらも数学の問題を解く上ではあまり良い態度とは言えません。読まずに解けたら天才ですが(笑)
まずは必要な情報を整理しながら問題文を細切れに読んでいきましょう。
一直線のジョギングコース上に、P地点とそこから2700m離れたQ地点があり、このコースをP地点からQ地点に向かって1200m進んだところにR地点がある。
これを言われた通りに図に表してみましょう。
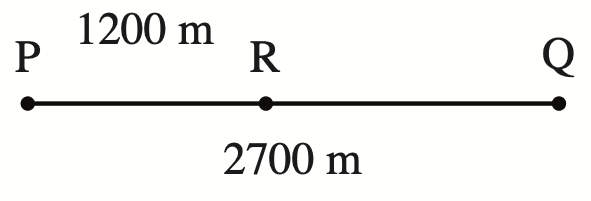
こんな感じで位置関係をざっくりと把握しておきましょう。
AさんとBさんは、同時にP地点を出発し、このコースをR地点までそれぞれ一定の速さで歩いた。BさんはAさんより5分遅くR地点に着いた。
大事なことは上の太線で示した部分です。そして、問題で与えられている図1が、AさんがP地点を出発してからR地点に着くまでの時間とAさんの歩いた距離の関係です。つまり「図1からAさんの速度が分かる」ということです。このグラフに上の枠内の情報を付け加えてみましょう。次のようなグラフが描ければ正しく情報を読み取ることができています。
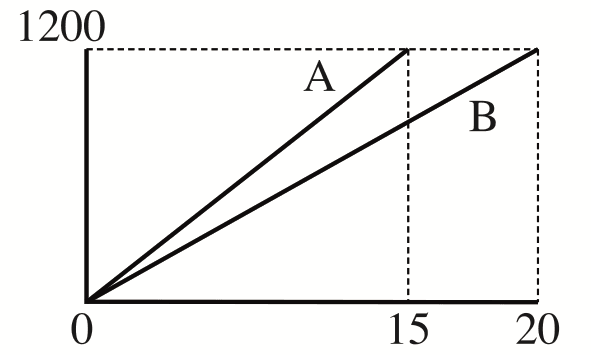
このグラフから、Aさんの速度は80m/分、Bさんの速度は60m/分であることが読み取れます。これで(1)は $80\times 3=240$ と求められますね。
次に図2を考えていきましょう。このとき、あわせてCさんの情報も考えます。
Cさんは、Aさんたちと同時刻にQ地点を出発し、このコースをR地点に向かって一定の速さで5分間走った後、5分間休憩し、一定の速さで歩いて、Aさんと同時にR地点に着いた。
とCさんは面倒な動き方をしていますが、結局のところ
図2は、AさんがP地点を出発してから $x$ 分後のAさんとCさんの距離を $y$ mとして、AさんがP地点を出発してからR地点に着くまでの $x$ と $y$ の関係をグラフに表したものである。
とあるので、図2を考えればいいということを把握して下さい。
文章で考えにくいものを図表やグラフを用いて考えるのは数学の常套手段ですよ!
(2)は $5\leqq x\leqq 10$ の範囲の直線の方程式を求めればOKです。
これについては、直線が通過する2点 $(5,\ 1300)$、$(10,\ 900)$ が分かっているので、ここから直線の方程式を求めていきましょう。
この2点の情報から、$x$ が $5$ 増加するあいだに $y$ が $-400$ 増加( $400$ 減少)することから、直線の傾きは $\displaystyle \frac{-400}{5}=-80$ であることが分かります。つまり、$y=-80x+a$ のように表せます。
この直線が上の2点 $(5,\ 1300)$、$(10,\ 900)$ を通過するのでどちらかを代入します。計算が簡単そうな後者を代入してみると
$$900=-800+a$$
となり、結局 $a=1700$ が得られ、求める直線の方程式は
$$y=-80x+1700$$
となります。
さて、問題は(3)です。
AさんとBさんの間の距離と、AさんとCさんの間の距離が等しくなるのは、AさんがP地点を出発してから何分何秒後か
ということですが、AさんとCさんの間の距離については図2から考えることができます。
しかし、AさんとBさんの間の距離についてはグラフがないので、先ほどのAさんとBさんの速度から考えていく必要があります。
$x$ 分後にAさんが進んだ距離は $80x$ であり、Bさんが進んだ距離は $60x$ ですから、$x$ 分後の2人の間の距離は $80x-60x=20x$ となります。
ここで、$y=20x$ のグラフを図2に書き込んでみると以下のような図が得られます。
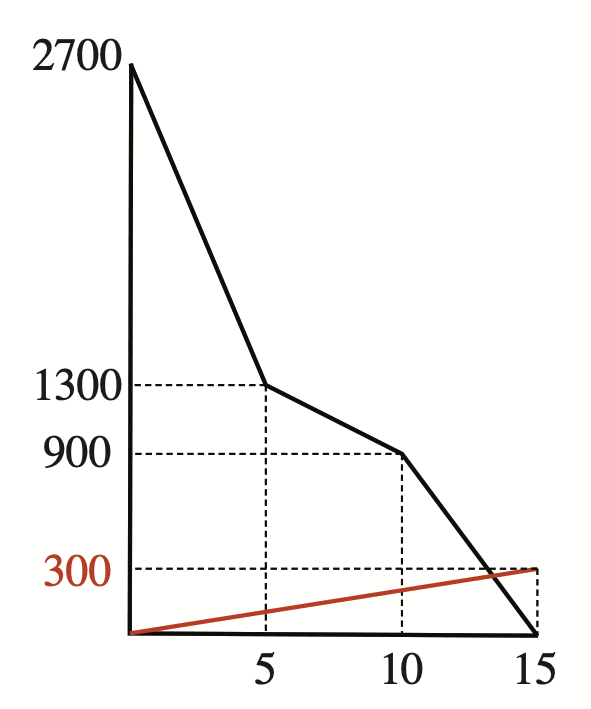
大切なのは $y=20x$ のグラフをなるべく正確にかくことです。$x=15$ のとき $y=300$ となるので図の赤い直線が $y=20x$ のグラフとなります。そうすると、$10\leqq x\leqq 15$ の範囲で交点が現れることが視覚的に把握できます。
このとき、黒い直線(AさんとCさんの間の距離)の方程式は(2)と同様にして、$y=-180x+2700$ となります。
結局、AさんとBさんの間の距離とAさんとCさんの間の距離が等しいということは、$y=20x$ と $y=-180x+2700$ の $y$ が等しくなるということであり、
$$20x=-180x+2700$$
から、$\displaystyle x=\frac{27}{2}$ となることが分かります。
(3)では同じレベルのグラフ(2人間の距離を示すグラフ)を用意して考えるというのがポイントになります。このように、情報は与えられているもののレベルが異なる情報である場合に解けなくなってしまう人が多いように思います。手元にある情報から、さらに導けるものはないか、情報のレベルを統一できないかという視点は持っておかなければなりません。「みはじ」だの「はじき」だのを利用して計算しているような人は、こういう問題になると途端にできなくなるので要注意です!
大問4
内容 方程式
難易度 標準
見た目は最近よく見かけるタイプの方程式の問題ですがちょっと面倒な問題です。面倒な理由は、与えられている情報が「4人分の材料」であるということです。この点を忘れると間違えてしまいます。
理科などの問題でもそうですが、単位量(1つあたりとか1gあたりとかの量)を意識することはとても大切です。
とりあえず、問題として与えられているのは「牛肉2300 gとじゃがいも13個を使った」というものだけなので、それ以外の材料は無視しましょう。ビーフシチューと肉じゃがで、それぞれ1人分がどれだけかを求めておくと見通しがいいでしょう。
| ビーフシチュー(4人) | ビーフシチュー(1人) | 肉じゃが(4人) | 肉じゃが(1人) | |
| 牛肉 | 600g | 150g | 400 g | 100g |
| じゃがいも | 2個 | 1/2個 | 4個 | 1個 |
ビーフシチューを $x$ 人分、肉じゃがを $y$ 人分作った場合、牛肉とじゃがいもについて、
$$\begin{cases}150x+100y=2300\\\frac{1}{2}x+y=13\end{cases}$$
という関係式を作ることができます。あとはこの連立方程式を解けばOKです。
一方で、とくに何も考えずに
$$\begin{cases}600x+400y=2300\\2x+4y=13\end{cases}$$
として、$\displaystyle x=\frac{5}{2}$、$y=2$を求めてから、$\displaystyle \frac{5}{2}\times 4=10$、$2\times 4=8$ と求めることも可能です。
後者の解答の場合に採点がどうなるんでしょうか? 私が採点するのであれば点は入りますが、説明がないと減点とかあり得そうですね・・・。
大問5
内容 作図
難易度 易
いつものように作図の問題では等距離を意識することが大切です。
この問題でもレベルを統一することがポイントになります。つまり、$l$ 上にない点Cを $l$ 上に移動させて1つの直線上の問題にすり替えることが重要となります。これはBを中心としてCを通る円を描き、$l$ と交わるところにDをとって考えればOKです。
そうすると、$\mathrm{AP=DB+BP}$ つまり $\mathrm{AP=DP}$ となる点Pを求めればいいことになります。
これは、AとDの垂直二等分線を作図すればOKですね。
垂直二等分線が描けないなんて人は要復習ですよ!!基本の作図はきちんと押さえておきましょう。
大問6(復習オススメNo.2)
内容 平面図形
難易度 やや難
正三角形を題材とした平面図形の問題です。きちんと理解しておけば力がつく問題だと思うので、できなかった人はじっくりと時間をかけて考えてみるといいでしょう。とくに(1)は、ただ解くだけなら何ということもない問題ですが、そこからいろいろと発展させることができる問題です(相似を学んだらもう1回やってみるといいでしょう)。
(1)は $\triangle \mathrm{MDE}$ の面積を求める問題です。パッと図を見たときに、直感的に「MDの長さが分かると求められるな」と感じられるかどうかが重要です。ちなみに、MDがBEと垂直に交わることはきちんと説明できますので気になる人は考えてみてください(BDとDEはどうなりますかね?)。
$\mathrm{BE=AD}=4\sqrt{3}$ は分かると思いますが、MDは簡単には求まりません。
面積の問題については直接求められる場合とそうでない場合があります。つねに、どちらの場合にも備えておきましょう。直接求められる場合は各種の面積公式などを利用することになりますが、そうでない場合にはいろいろな角度から考えていく必要があります。
ここでは、中点という条件があるためこれを上手に利用することを考えてみましょう。中点を利用した面積の考え方は下の三角形の面積公式と図から分かることを理解しておくことが大切です。
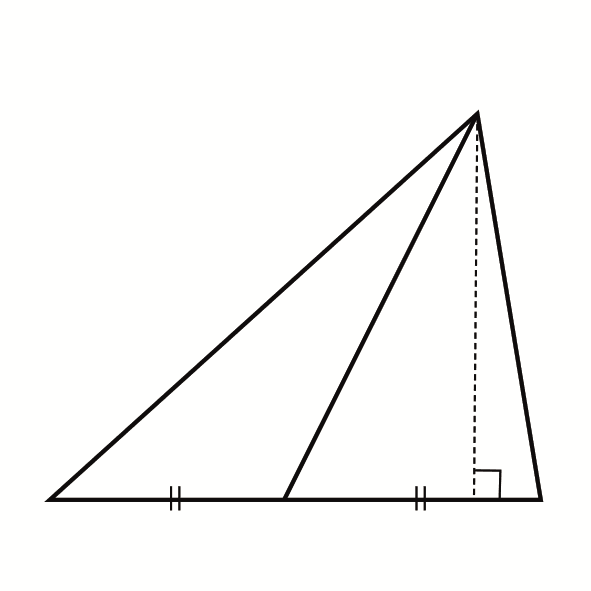
$\displaystyle \frac{1}{2}\times $底辺$\times$高さ
上の図では底辺の中点をとって三角形を2つに分けていますが、この2つの三角形の面積は等しくなることが理解できていれば大丈夫です。この2つの三角形は、高さが同じ(点線の長さ)であり、底辺も同じ値になることから面積が等しくなります(この考え方を発展させると「底辺の比」が「面積比」と等しくなるような場合も考えられるようになります)。
これによって、
$\displaystyle\triangle\mathrm{BCE}=\frac{1}{2}\times \triangle\mathrm{ABC}$
$\displaystyle\triangle\mathrm{BDE}=\frac{1}{2}\times \triangle\mathrm{BCE}$
$\displaystyle\triangle\mathrm{BDE}=\frac{1}{2}\times \triangle\mathrm{BCE}$
$\displaystyle\triangle\mathrm{MDE}=\frac{1}{2}\times \triangle\mathrm{BDE}$
と芋づる式に面積を求めていくことができます。
(2)の合同の証明は簡単なので大丈夫でしょう。$\triangle\mathrm{ABC}$ が正三角形であることを忘れないように!
(3)については、解説を読んでもらえれば問題ないと思います(手抜きではないです笑)。
この先、平面図形の問題では面積比や線分比を考える問題が増えていきます。そのため、面積について、あるいは比についてきちんと復習をしておくと良いでしょう。私の指導経験からすると、とくに比についてはよく分かっていない人が多すぎます!
大問7
内容 空間図形
難易度 やや易
時間的に空間図形は手をつけなかったという人も多いかもしれませんが、空間図形の問題は見た目がゴツくても解いてみるとどうということはないレベルの問題もあります。見た目だけで判断しないことが大切です。
(1)はねじれの位置の問題なので、問題なく解けてほしいところです。
(2)の表面積の問題では、3つの長方形と2つの三角形の面積を足していくだけなのですが、大切なことは2つに分けた立体がどのような立体になるかを瞬時に把握することです。
これについては、うまい解法といったものは存在しません。そのため正答率が極端に低くなります。
図を描く練習(展開図や見取り図など)だけでなく、実際に立体を切り分けてみる「感覚」が大切になります。粘土などを使って実際に立体を切断してみて、立体がどうなるか、切り口がどうなるかを確認してみるといいでしょう。
(3)も必要なことは(2)と同じです。まずは切り取られた立体がどのような形になるかをよく考えてみましょう。
さらに、体積もすぐに求められるとは限りません。面積や体積は簡単な形については公式を利用して求められますが、複雑な形状になってくると公式だけではどうにもならなくなります。その際に大切なことは「単純な形に分割する」ということです。
ここでも求める立体を「さらに自分で切り分ける」ことが必要となります。ここではBを通ってEFHに平行な平面で切断すると、下側が三角柱、上側が四角錐となり比較的簡単な形になります。
今回の空間図形は比較的簡単な問題でした。
まとめ
50分という試験時間を考えると、全ての問題を解き切るのはなかなか大変なセットです。そこまで難しい問題はありませんが、考える時間を考慮すると2/3くらいで時間切れとなったという人が多かったのではないかと思います。また半分程度しか解けなかったという人も相当数いるでしょう。満点が狙えないわけではありませんが、現実的に考えると8割程度でも十分な学力があると考えられます。
数学が苦手だという人は、まず計算のルール(小学生の内容から!)を1からやり直してみましょう。また、比較的簡単な知識だけで解けるような単問形式の問題をやって大問1でしっかりと得点できるようにしておくことが大切です。難しい問題が多いからといって、難問ばかりの問題集に手を出しても意味がありません。
また、数学が得意な人は、模範解答とは異なる考え方ができないかを検討してみたり、条件を変えるとどうなるかを考えてみたりするのも理解を深める手助けとなるでしょう。
点数が欲しいからといって「たくさんのパターンに慣れておこう」などと考えるのは愚の骨頂です。そんなものを数学の勉強だと思ってしまうと後で面倒なことになります。高校入試を乗り切ってしまえばいい、という考え方の人はそれでも良いかもしれませんが、将来は理系へ進みたいと考えているような人は「考える」という行為に積極的であってもらいたいなと思います。そういう意味で、復習を徹底的にやってみることが大切だと思います。


