2025第1回石川県総合模試の数学を解いてみた

今年もいよいよ総合模試が始まりました。第1回石川県総合模試を受験された受験生のみなさん、お疲れ様でした〜
7月6日(日)に2025年度第1回石川県総合模試が実施されました。
石川県総合模試は、毎年多くの受験生が受験する重要な模試となっています。石川県の公立高校入試の形式に近く、難易度も高めの問題が多いため、入試対策の一環として受験することをおすすめします。
というわけで、今年度の第1回の模試だったわけですが、こうした入試レベルの模試を受けるのは初めてという人が多かったのではないかと思います。そのため「全然できなかった」とショックを受ける人もそれなりにいます。
当塾の塾生も、時間が足りないとか、あり得ないミスをしたとか色々言っていました笑。
本番の入試はまだまだ先の話なので、現時点の成績はあまり気にしないようにしましょう。それよりも、ここからどうやって学力アップに繋げていくかを考える方が重要ですよ!
概観
第1回の数学の出題数は大問数が7(うち小問数23)でした。実際の入試で大きな変更がない限り、問題数はほぼこの形で固定されています。
全体的な内容としては、問題集などでも良く取り上げられる典型問題から、思考力が必要とされるやや高度な問題までバラエティに富んだ内容となっています。また、実際の入試同様、計算の過程を記述させる問題や証明などの説明を求められる問題が多いため、試験時間内に全ての問題を解き切るのは難しい分量・難易度となっています。
70点台後半で上位層に入るくらいの得点分布となります。ちなみに、昨年度の第1回の数学は平均点が34.5点という結果でした。
したがって、全部解けなくて当然くらいに考えておきましょう。全部に手をつけようとして雑な考え方になってしまうと、それはそれは別の問題が生じてしまうので要注意です。
入試の指導において、よく「問題を見たら瞬時に解き方を思いつけるようにする」などと主張する指導者がいますが、近年の入試問題では解き方がすぐに分かるような典型問題はあまり出題されない傾向があります。解き方よりも先に手を動かしながら具体例を書き出したり、図をかいて考えるといったことを徹底していく方が良いでしょう。
また、中学生の数学力は近年、悲惨なほどに低下してきています。そうした状況もあって、模試の問題の難易度は以前よりもかなり易しくなってきています。そのため、いわゆる入試テクニックのようなものや、特別な知識などを必要とする問題はほぼ出題されません。それよりも、しっかりとした基礎力があるかどうかを試されると考えておきましょう。
なお、基礎=簡単ではありません。基礎力をつけるという話になると、簡単な問題をたくさんやればいいと勘違いする人がいまだにたくさんいますが、それは違います!
また、模試は入試本番の予行練習的な意味もあるので、時間配分であったり手をつける問題の優先順位であったりを考えながら受験することも重要です。何となく受験して点数と判定だけを見て終わっていては全く意味がありません。本番までにしっかりとした学力をつけるためにも、復習を早めにやって、足りない部分を補っていくことを意識してください。
全体的な難易度標準
問題の解説
ここからは問題の具体的な解説となります。問題用紙を準備してご覧ください。
大問1
内容小問集合
難易度易
大問1は計算力や基本的な知識を問う小問集合となります。ここは、どの生徒も満点を狙っていきたいところです。とくに数学が苦手だという人は、大問1の得点が現実の入試でも重要なウエイトを占めるので、しっかりと復習をやってミスなく乗り切れるようにしましょう。
(1)は単純な計算問題でした。この時期の計算問題では符号の取り扱いに十分注意しましょう。例年、ウ〜オは正答率が思った以上に低くなるため、間違えてしまった人は計算方法をよく見直しておきましょう。
計算ミスが多い人は、丁寧に計算をするよりもできるだけ計算をしないような工夫を考えると良いでしょう。
(2)は単純な代入の問題です。ここは問題なくできた人が多いでしょう。とくに解説も必要ないと思われます。
(3)は度数分布表に関する問題でした。

階級値が7.5となる階級は5〜10の階級です。この階級の度数は7となるので、相対度数は$\displaystyle\frac{7}{35}=0.2$となります。
(4)は確率の問題でした。2個のサイコロをふるので、全部で36通りの目の出方があります。赤のサイコロの目が $a$、白のサイコロの目が $b$ なので、これを $(a,\ b)$ のように表すことにします。$2a+b=10$ となるのは
$$(a,\ b)=(4,\ 2),\ (3,\ 4),\ (2,\ 6)$$
の3通りなので、求める確率は $\displaystyle\frac{3}{36}=\frac{1}{12}$ となります。
すべてのパターンを書き出して考えるのが基本ですが、ここでは $2a$ が偶数であることに着目して、$b$ も偶数でなければならないことから絞っていくと良いでしょう。
(5)は角度の問題でした。図のような条件が与えられたときの $x$ を求める問題でした。
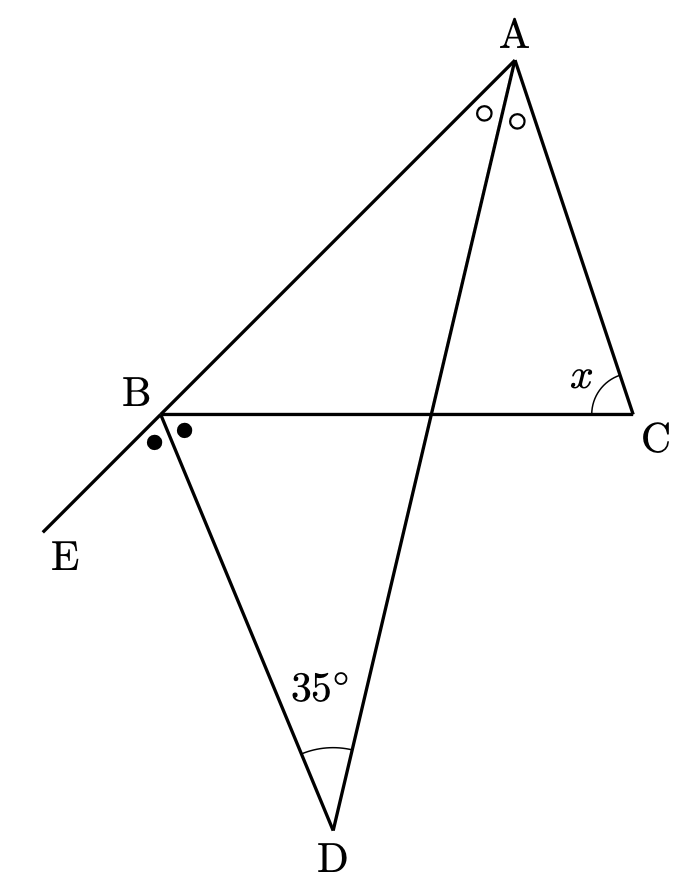
ここでは三角形の外角に着目することで、$\circ$ と $\bullet$ の関係が見えてきます。
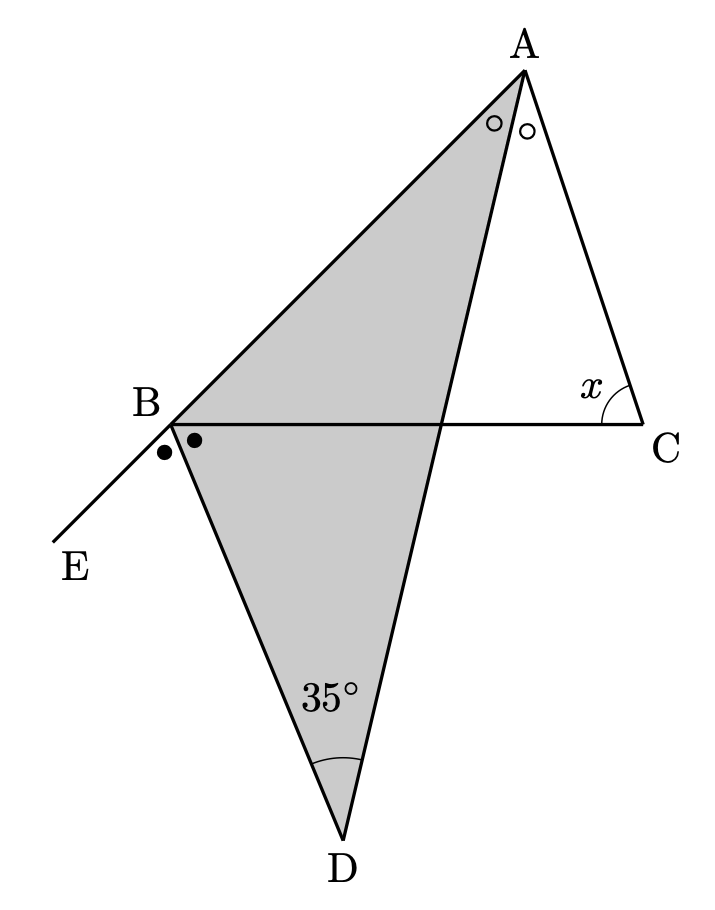
図の三角形 $\mathrm{ABD}$ に着目すると、外角 $\angle\mathrm{EBD}$ について
$$\bullet=35^\circ+\circ$$
という関係が得られます。
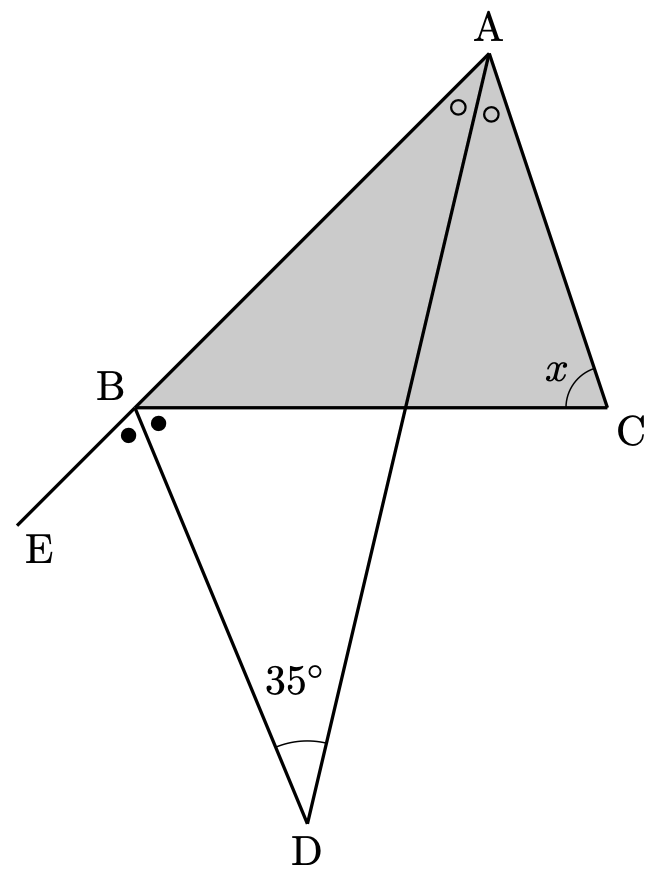
同様に三角形 $\mathrm{ABC}$ に着目すると、外角 $\angle\mathrm{EBC}$ について
$$2\times \bullet=x+2\times \circ$$
となります。これを整理して
\begin{gather*}
2\times (35^\circ+\circ)=x+2\times \circ\\
2\times \circ +70^\circ=x+2\times \circ
\end{gather*}
よって、$x=70^\circ$ となります。
大問2(復習おすすめNo.3)
内容規則性
難易度易
大問2は規則性の問題でした。大問2は規則性以外にも確率や統計などの問題が出題されることもあります。難易度は低めの問題が多いですが、案外、ここで点を落としてしまう人がいるので気をつけましょう。
大切なことは、具体的に書き出して考えてみることですよ! いきなり数式で表そうとするのではなく、まずは目の前で起こることを確認することが大切です。
今回は、正方形を並べて階段を作る問題でした。
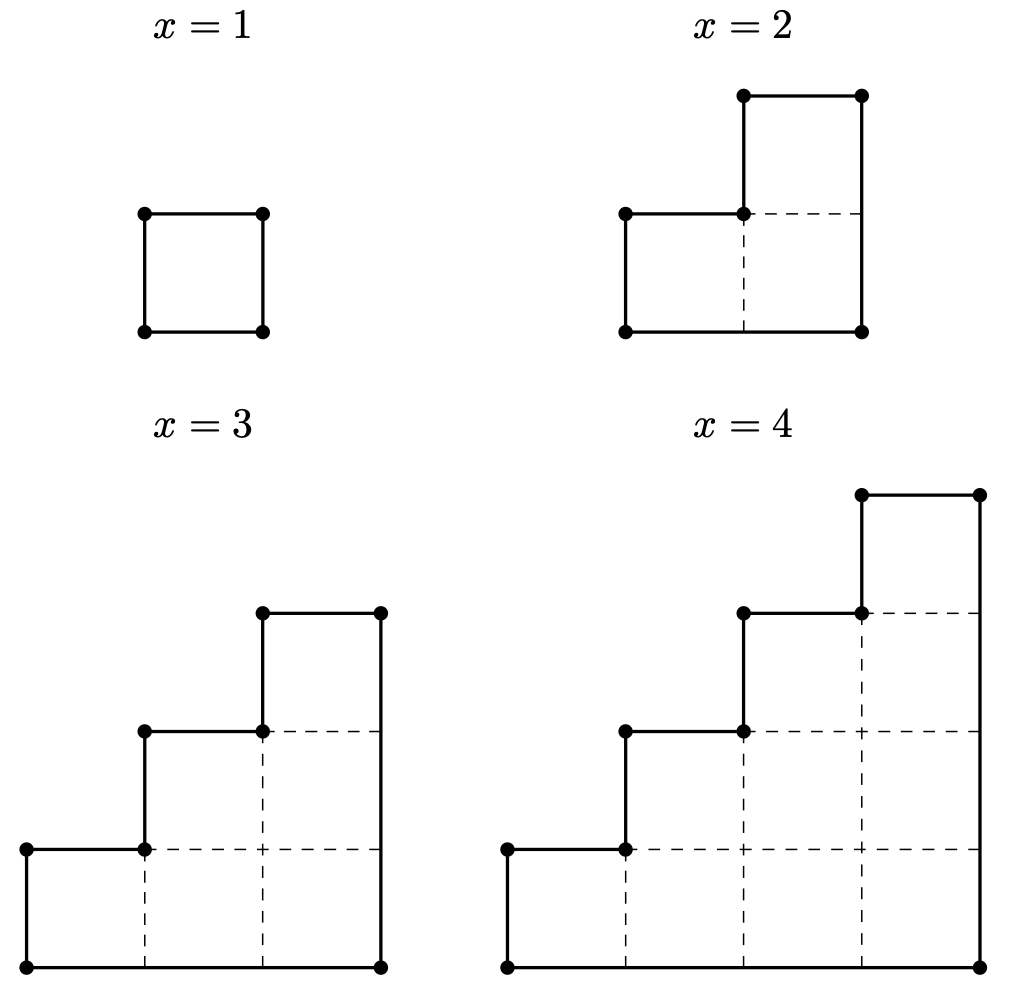
図のように、階段の段数が $x$ 段となるときの様子を考える問題でした。
(1)はおそらくほとんどの人ができたのではないかと思います。図をかいてしまえばすぐにわかります。
こういう問題で、図を描かずに思考停止している人を見かけますが、数学に対する取り組み方を根本的に間違っている可能性が高いので気をつけてくださいね!
図は描いてしまえばすぐに答えが分かるので、ここでは計算によって考えてみます。
まずは規則を見るために、整理して書き出してみます。
\begin{align*}
\begin{array}{|c|c|}\hline
x&y\\\hline
1&4\\\hline
2&6\\\hline
3&8\\\hline
4&10\\\hline
\end{array}
\end{align*}
$x=2$ のときは、4に2を1回加えて6となります。$x=3$ のときは、4に2を2回加えて8となります。$x=4$ のときは、4に2を3回加えて10となります。ということは、$x=10$ のときは、4に2を9回加えて$$y=4+2\times9=22$$
となります。
この規則を一般化しておくと、$x=n$ のときは$$y=4+2(n-1)$$となります。
(2)は簡単ですね。図から考えれば一発でしょう。横は $200$ となり、縦はそれに $+1$ することになるので
$$\frac{200\times 201}{2}=20100$$
階段を2つ用いて面積を出しているので、2で割ることを忘れないようにしましょう。
この問題は等差数列とその和を題材としています。興味がある人は、(2)の内容を一般化してみると良いでしょう。等差数列の和の求め方が見えてくるでしょう。シンプルですがなかなか良い問題でした。
大問3
内容関数
難易度易
大問3は関数(反比例)の問題でした。(3)が少し面倒に感じた人がいたかもしれませんが、全体としては易しい問題でした。上位校狙いの人は満点を取っておきたいところです。
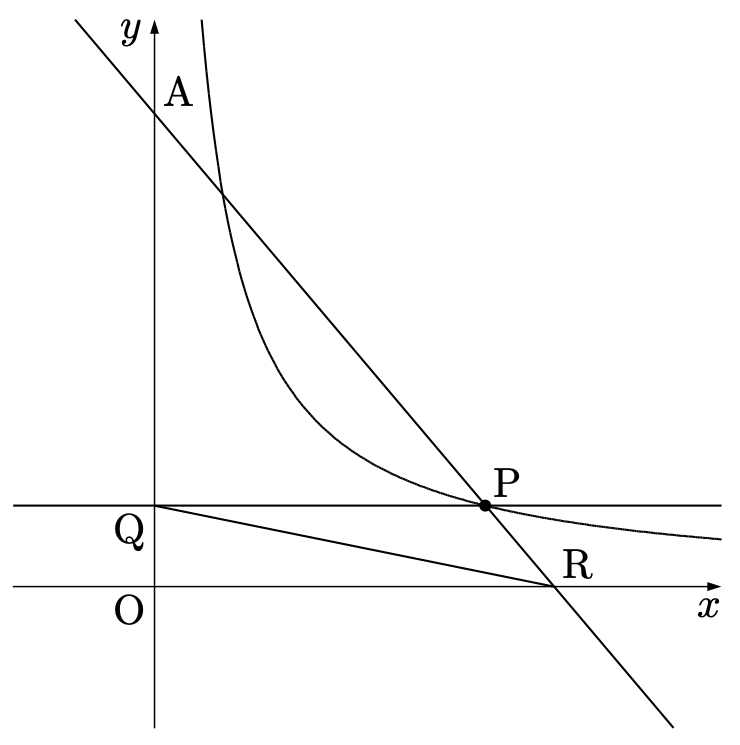
グラフは $\displaystyle y=\frac{12}{x}\ (x>0)$ で $\mathrm{A}$ の $y$ 座標は $10$、$\mathrm{P}$ はグラフの $y$ 座標が $10$ より小さい部分を動く点です。また、$\mathrm{P}$ を通って $x$ 軸に平行な直線と $y$ 軸の交わる点が $\mathrm{Q}$、直線 $\mathrm{AP}$ と $x$ 軸との交点が $\mathrm{R}$ となります。
(1)は問題ないでしょう。
$$4=\frac{12}{x}$$
より、$x=3$ となります。
よって、$\mathrm{P}(3,\ 4)$ となり、求める直線の傾きは $\displaystyle\frac{-6}{3}=-2$ なので、直線の式は
$$y=-2x+10$$
となります。
$y=ax+b$ とすると面倒なだけです。$y$ 切片は最初から分かっているので、傾きだけ考えば十分です。
(2)は $\mathrm{AQ=OQ}$ という条件が与えられます。これは、すなわち $\mathrm{Q}(0,\ 5)$ ということです。
したがって、あとは(1)と同様にして
$$5=\frac{12}{x}$$
より、$\displaystyle x=\frac{12}{5}$ となります。
(3)は $\mathrm{P}$ の $x$ 座標が $6$ のとき、$\triangle\mathrm{APQ}$ の面積が $\triangle\mathrm{PQR}$ の何倍かを求める問題です。
$\mathrm{P(6,\ 2)}$ はすぐに求められます。とりあえず、邪魔な線を消してシンプルな図を描いてみましょう。

$\triangle\mathrm{APQ}$ も $\triangle\mathrm{PQR}$ もともに底辺を $\mathrm{PQ}$ と見れば、高さはそれぞれ $\mathrm{AQ}$、$\mathrm{QO}$ となります。この高さの比がそのまま面積比となるので
$$\triangle\mathrm{APQ}:\triangle\mathrm{PQR}=8:2=4:1$$
したがって、$4$ 倍となります。
大問4
内容方程式
難易度易
大問4の方程式の問題も非常にシンプルで易しい問題でした。
A店は商品Pを20個までは割引なしで販売し、20個を超える分については10%引きで販売し、B店は個数に関係なく一律で $a$ %引きで販売するという設定です。
(1)は商品Pの定価を $x$ 円とし、A点で商品Pを50個買ったときの金額を表す問題でした。
設定どおりに考えましょう。20個までは割引なしなので、料金は $20x$ となります。残りの30個については、10%引きとなるので、$30\times 0.9x=27x$ となります。
したがって、合計の金額は $47x$ となります。
(2)は、A店とB店で商品Pの定価が同じとき、それぞれの店で商品Pを50個ずつ買った場合に同じ金額となるような $a$ の値を求める問題でした。
(1)ですでにA店の金額を求めているので、あとはB店の金額を求めて等号で結ぶだけです。
$$47x=50x\left(1-\frac{a}{100}\right)$$
これを解けば $a=6$ が得られます。
大問5
内容作図
難易度易
大問5は作図の問題でした。作図の問題はかなり難易度の幅があるのですが、今回は易しい問題でした。
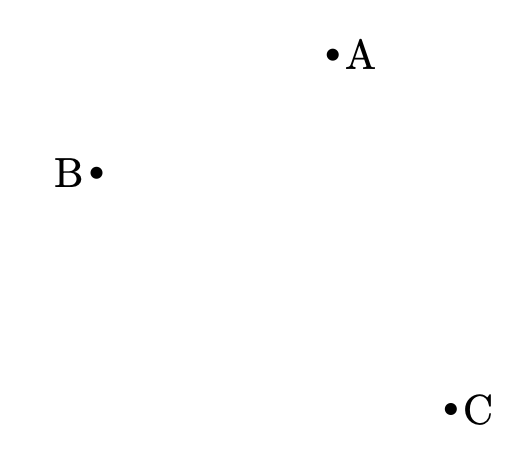
条件は2つです。
- 線分 $\mathrm{AB}$ の垂直二等分線を $l$ とすると、点 $\mathrm{P}$ は $l$ 上にある。
- $CP\perp l$
1.は線分の垂直二等分線の作図となります(下図)。
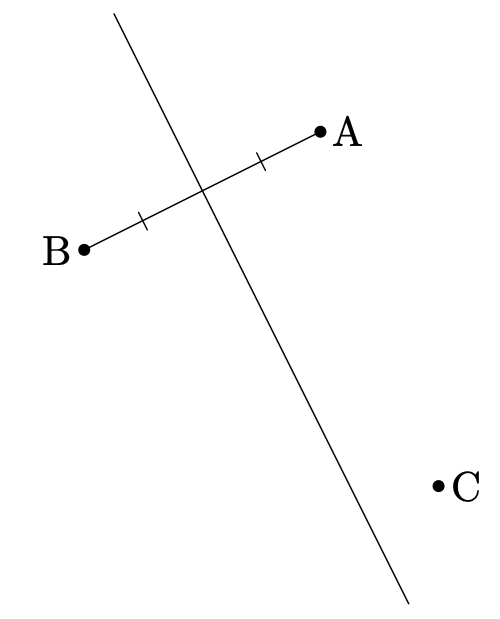
2.は、Cから直線 $l$ に垂線を引く作図です。どちらも基本的な作図なので、簡単にできた人が多かったのではないかと思います。
作図が苦手な人は、まず図形の知識に穴がないかを確認しましょう。その上で、基本の作図をどう組み合わせていけば良いかを考えるようにしましょう。
大問6(復習おすすめNo.1)
内容平面図形
難易度標準
大問6は平面図形の問題でした。二等辺三角形が重要な役割を果たす良問でした。この問題はよく復習しておきましょう。
下図のような平行四辺形 $\mathrm{ABCD}$ が与えられています。長さや面積の単位は省略します。
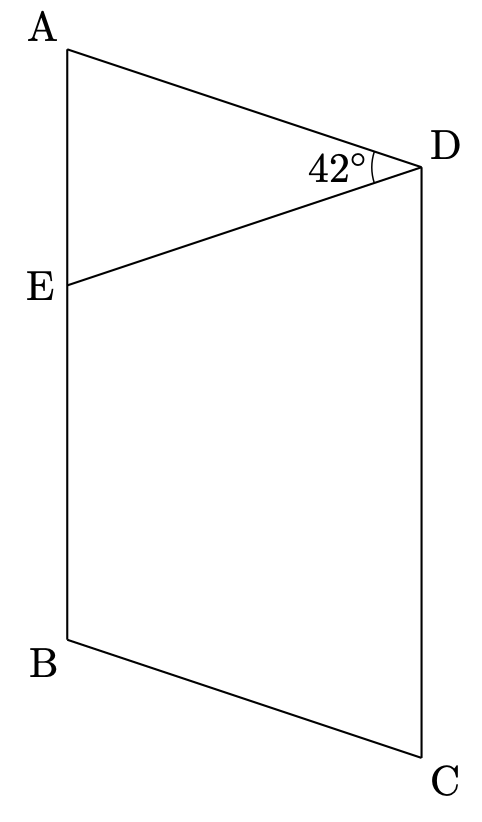
(1)は $\mathrm{AD=ED}$、$\angle\mathrm{ADE}=42^\circ$ のときの $\angle\mathrm{EDC}$ の角の大きさを求める問題でした。
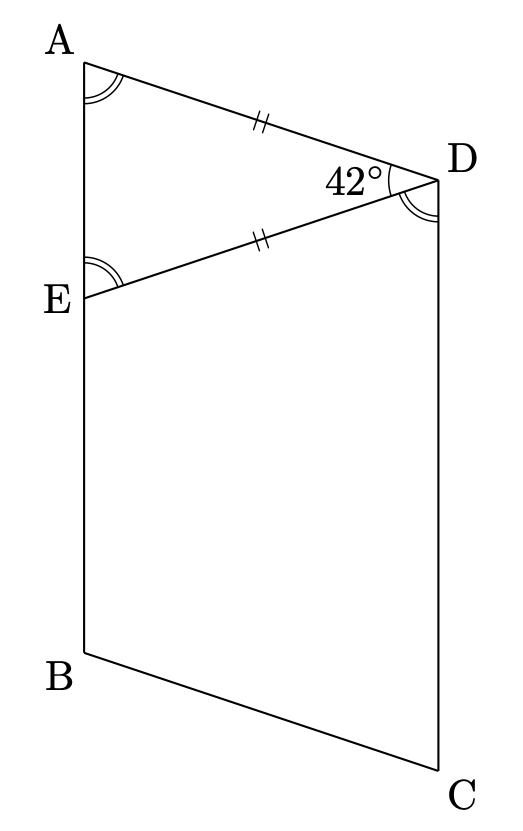
二等辺三角形と錯角に着目すると上図のようになります。よって、$\angle\mathrm{EDC}$ の大きさは
$$\frac{180-42}{2}=69$$
となります。
(2)は $\mathrm{AE=CF}$ のとき、$\triangle\mathrm{AED}\equiv \triangle\mathrm{CFB}$ となることを証明する問題でした。
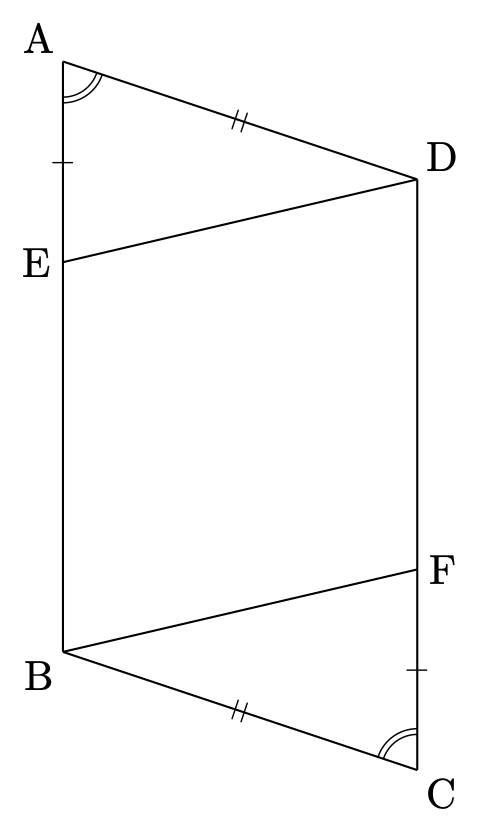
四角形 $\mathrm{ABCD}$ が平行四辺形であることから
\begin{gather*}
\mathrm{AD=CB}\\
\angle\mathrm{EAD}=\angle\mathrm{FCB}
\end{gather*}
となり、$\triangle\mathrm{AED}\equiv \triangle\mathrm{CFB}$ がすぐに示せます。
(3)は難しく感じた人も多かったのではないかと思います。
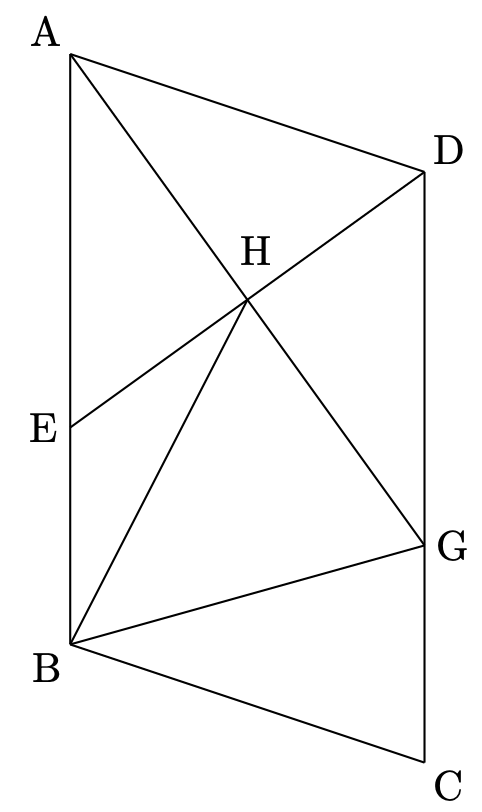
図において、$\angle\mathrm{BAD}$ の二等分線と辺 $\mathrm{CD}$ の交点を $\mathrm{G}$、線分 $\mathrm{AG}$ と線分 $\mathrm{DE}$ の交点を $\mathrm{H}$ とし図のように結びます。このとき、$\triangle\mathrm{AGD}$ の面積が $35$、$\mathrm{AG\perp DE}$、$\mathrm{AB:AD}=10:7$ としたときの、$\triangle\mathrm{BGH}$ の面積を求める問題でした。
条件が多いので、とりあえず書き込んでいきましょう。

ここから、$\triangle\mathrm{AED}$ が二等辺三角形($\triangle\mathrm{AHE}\equiv \triangle\mathrm{AHD}$ がすぐに示せます)であること、平行四辺形であることから錯覚が等しくなることを考えて、下図のように考えていくことができます。

$\triangle\mathrm{AHD}\equiv \triangle\mathrm{GHD}$ もすぐに示せるので、$\triangle\mathrm{ADG}$ も二等辺三角形となることが分かり、図のように $\mathrm{DG:GC}$ が分かります。また、$\mathrm{AH=HG}$ も忘れずにチェックしましょう。
このとき、$\triangle\mathrm{ADG}$ と $\triangle\mathrm{BCG}$ は高さの等しい三角形であり、底辺の比がそのまま面積比となります。したがって、
$$\triangle\mathrm{ADG}:\triangle\mathrm{BCG}=7:3$$
ゆえに、$\triangle\mathrm{BCG}=15$ となります。また、$\triangle\mathrm{BCG}$ と $\triangle\mathrm{ACG}$ は同じ面積となることから、結局 $\triangle\mathrm{ADG}$ と $\triangle\mathrm{BCG}$ の面積の和 $35+15=50$ が平行四辺形の面積の半分となります。
次に、$\triangle\mathrm{ABG}$ に着目します。ここでも、高さの等しい三角形に着目すると$\triangle\mathrm{ABG}=\triangle\mathrm{ABC}$ となります。
よって、$\triangle\mathrm{ABG}=50$(平行四辺形の半分)となることが分かります。
また、$\mathrm{AH:HG}=1:1$ となることから
$$\triangle\mathrm{ABH}=\triangle\mathrm{BGH}=25$$
となることが分かります。よって、求める面積は $25$ となります。
この問題では、二等辺三角形の頂角の二等分線は底辺を垂直に二等分するという性質が重要な役割を果たしていました。
このあたりの図形の知識が曖昧な人は、夏休みを利用してよく復習をしておきましょう。
大問7(復習おすすめNo.2)
内容空間図形
難易度標準
最後は空間図形の問題でしたが、時間がなくて解けなかったという人も多かったと思います。(1)、(2)は平易な問題だったので、ここだけでも解いておきたいところです。(3)の体積を求める問題は、典型的な問題なのでよく復習をしておきましょう。

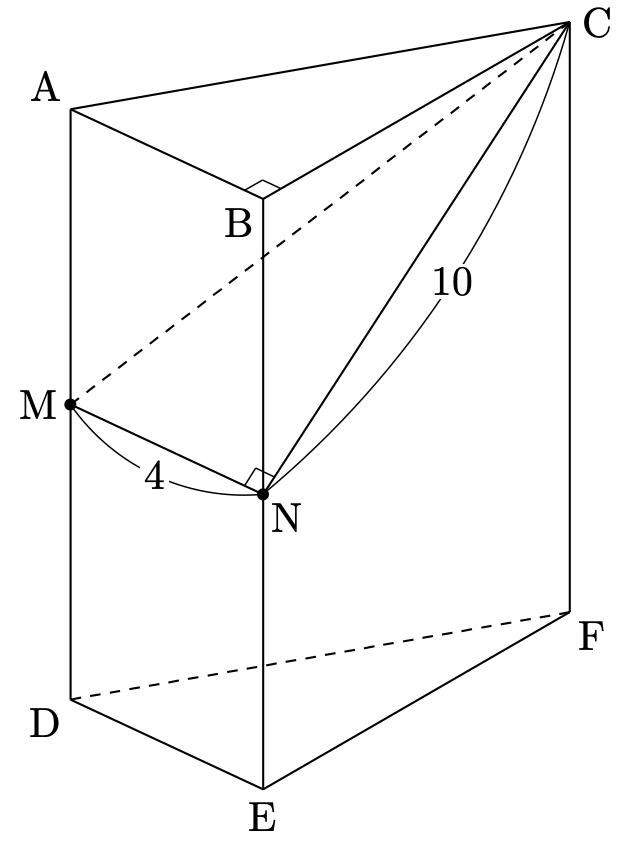
図のような三角柱が与えられていました。$\mathrm{M}$、$\mathrm{N}$ は中点です。
(1)は解説不要でしょう。$\mathrm{AD}$ がどこにあるかを考えれば問題なくアとキが選べるでしょう。
(2)もサービス問題でした。下図の $\triangle\mathrm{CMN}$ の面積を求める問題です。
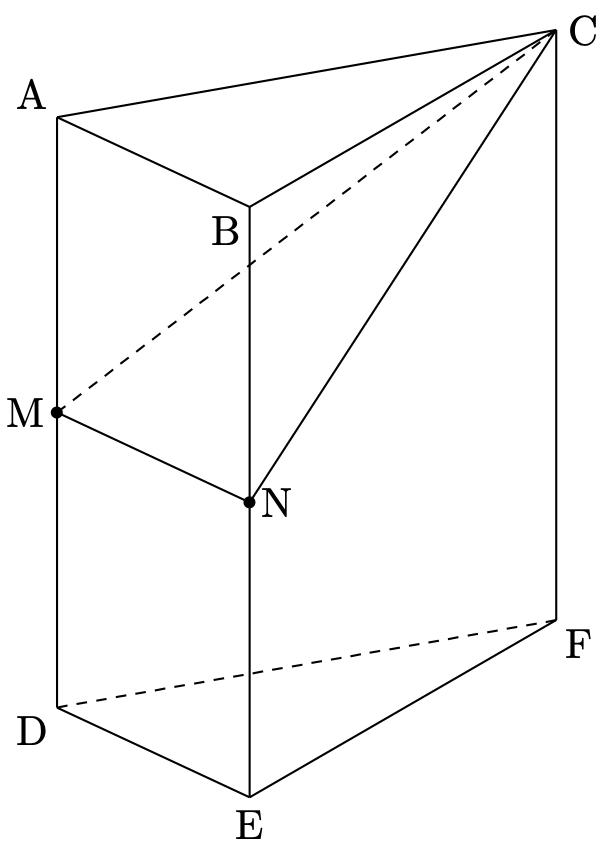
$\mathrm{CN}=10$ が与えられているので、$\angle\mathrm{MNC}=90^\circ$ に注意すれば簡単です。
求める面積は
$$\frac{1}{2}\times 4\times 10=20$$
となります。
(3)が少々面倒な問題です。下のような図が与えられます。$\mathrm{O}$、$\mathrm{P}$ は中点となっています。
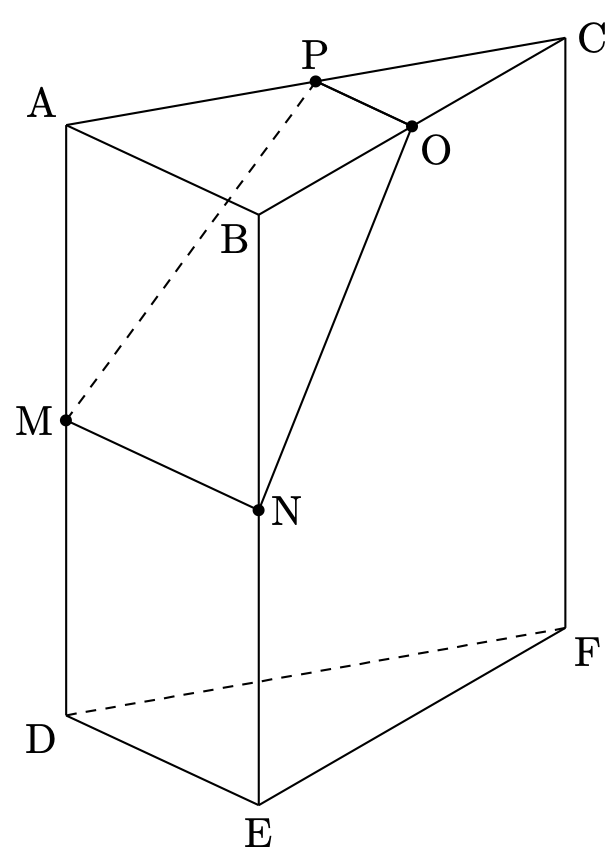
このとき、次の図の色付き部分の体積を求めよという問題でした。
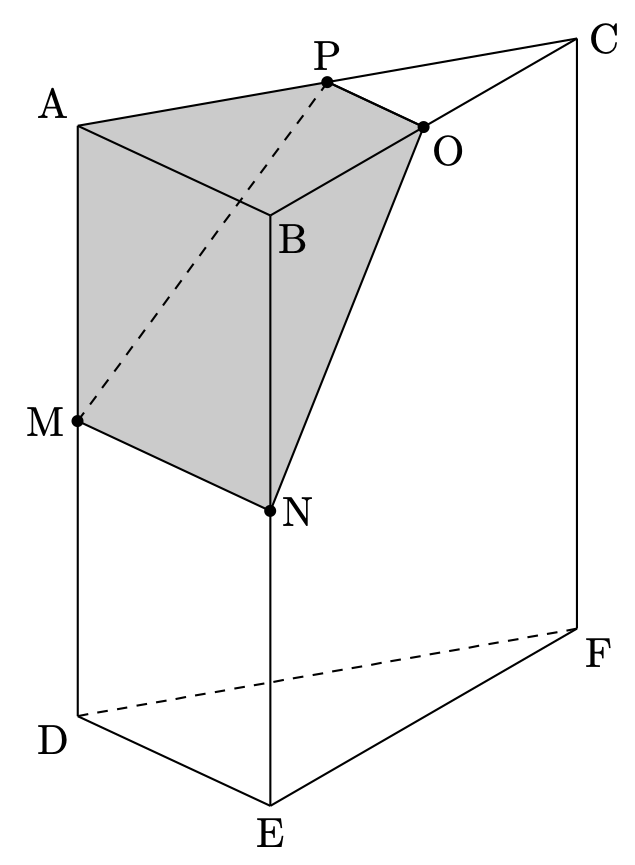
こんなヘンテコな形の立体の体積を直接求めることは無理です。こういう場合に、自分の求められる図形から考えていくというのが大切な思考になります。

図のように、平面 $\mathrm{PBN}$ で立体を切断すると、$\mathrm{N-POB}$ という三角錐と $\mathrm{P-ABNM}$ という四角錐に分割されます。
$\mathrm{N-POB}$ の底面 $\triangle\mathrm{POB}$ の面積から考えましょう。
2つの直角三角形に着目すると $\triangle\mathrm{POB}\equiv \triangle\mathrm{POC}$ が言えます。
また、$\triangle\mathrm{PCB}$ が高さの等しい三角形に着目することで $\triangle\mathrm{APB}=\triangle\mathrm{PCB}$ が言えます。
したがって $\triangle\mathrm{PCB}$ は $\triangle\mathrm{ABC}$ の半分となることが分かります。ゆえに、$\triangle\mathrm{POB}$ の面積は $\triangle\mathrm{ABC}$ の半分の半分、すなわち
$$\frac{1}{2}\times \frac{1}{2}\times \left(\frac{1}{2}\times 4\times 8\right)=4$$
となります。また、高さは $\mathrm{BN=6}$ となるので、$\mathrm{N-POB}$ の体積は
$$\frac{1}{3}\times 4\times 6=8$$
となります。
$\mathrm{P-ABNM}$ の体積は、底面となる四角形 $\mathrm{ABNM}$ の面積が $6\times 4=24$ であり、高さは $\mathrm{OB=4}$ となることから
$$\frac{1}{3}\times 24\times 4=32$$
よって、求める立体の体積は $40$ となります。
現時点ではかなり煩雑な計算を要しますが、もう少し勉強が進んで「相似」を学ぶともう少しラクになります。
まとめ
解いてみた第1印象は、ずいぶんと易しくなったなあという感じです。しかし、模試を受けたことのない受験生からすれば、それなりに難しいテストだったのではないかと思います。定期テストと比べて、問題の難易度が高く感じたかもしれません。また時間制限が厳しくて、半分くらいしか解けなかったという人もたくさんいたのではないかと想像します。
昨年も学力低下を考慮してなのか、かなり問題が簡単になったなと思っていたのですが、蓋をあけてみると平均点が34.5点という衝撃の結果となりました。今年度の中3生の学力がどの程度なのかはまだ分かりませんが、最近の数学力の低迷を考えると、そこまで平均は高くならないのではないかと思います。
これから、受験回数を重ねていけばある程度は慣れてくると思いますが、やはり図形の問題に対する理解不足は気になるところです。手っ取り早く合格点を取るために、前半で点数を稼ぐというのが受験生の常識のようになってきていますが、高校進学後に図形が大きな穴となってしまっている生徒をよく見かけます。実際の試験で解くかどうかは別として、普段の学習ではしっかりと図形の問題までやっておいてほしいなと思います。
というわけで、今年度も入試に向けたスタートが切られました。
まだまだ先は長いので一歩ずつ着実に理解を積み上げていきましょう!


