おうぎ形の面積のアレ

日が暮れるのが早くなってきました。気がつけば11月も半分をすぎました。歳をとったせいか、1年が本当に早く感じるようになりました。そして、気がついたら死んでいるんでしょうね(いつもコレ言ってんな)。
先日の金沢市統一テストの解説で触れた「おうぎ形の面積」の求め方についてサクッとお話ししておきたいと思います。
図のようなおうぎ形の面積の面積を $S$ としたとき、下のような関係が成り立ちます。
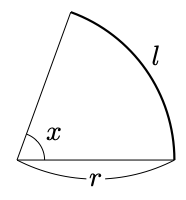
$$S=\frac{1}{2}lr$$
「え〜そうなんだ!便利!」で終わってはダメです。これが本当に正しいのかどうか、そしてどのように導かれるのかをきちんと理解しておかなければ意味がありません。こうした確認をやらずに何でも鵜呑みにしてしまうのは危険です。
ということで、実際に成り立つのかどうかを確認していきましょう。
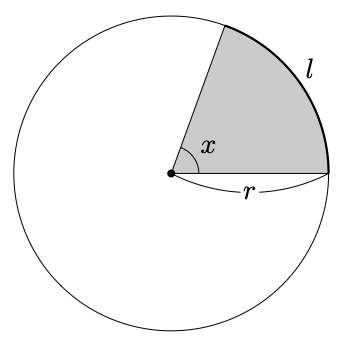
おうぎ形は円の一部と考えるのが基本的でしょう。
上の図で、円の面積は $\pi r^2$ となります。これを中心角 $x$ 分だけ切り取ればいいので
$$S=\pi r^2\times \frac{x}{360}$$
となります。基本的にはこれで十分です。
次に、おうぎ形の弧の長さ $l$ についても考えてみましょう。
基本的な考え方は面積と同じです。円周を求めて、それを中心角の分だけ切り取ります。
円周は $2\pi r$ となるので
$$l=2\pi r\times \frac{x}{360}$$
とすればおうぎ形の弧の長さが求まります。
この $l$ についての式を下のように変形します。
$$\frac{l}{2\pi r}=\frac{x}{360}$$
そして、先ほど求めた $S$ の式とから $\displaystyle\frac{x}{360}$ を消去すると
$$S=\pi r^2\times\frac{l}{2\pi r}=\frac{1}{2}lr$$
が得られます。
みなさんも、自分の手で確認できるようにしておくといいでしょう。
ちなみに、これを何の説明もなく「おうぎ形の面積の公式」などと言って大袈裟に取り上げている本は今すぐ捨ててOKです。
結果だけを丸暗記してその仕組みが全く分かっていないというのは、数学難民への最短距離となってしまうので要注意ですよ! とくに素直な中学生ほど、知らず知らずのうちにダメな方向へ誘導されている可能性が高いので、気をつけてくださいね。