場合分けの話

高校3年生は部活を引退した生徒が多く、受験勉強も本格化してくる時期です。自習に来る生徒も増えて来て、ああ、今年もいよいよだなあなんて思っています。まだまだ時間はありますが、油断しているとあっという間に時間が過ぎてしまうので計画的に進めていきましょう!
6月になり、高校1年生は2次関数の単元に入りました。
2次関数は高校数学の中でも最も大事な内容の1つであり、ここでしっかりと考える力をつけておくことが必要不可欠です。
とくにグラフをいろいろとかいて考えるということがこの先の多種多様な問題を考える上での土台となります。
しかし、そうした作業を面倒だと感じる人も多いようで、何とかパターンで乗り切ろうと考える人もいるようです。
まあパターンで考えることもできなくはないですが、問題がいろいろと変化するとかえってその方が面倒になりますよ、なんて話は通じないんですよね。なぜだ!?
そんなわけで、代表的な問題を考えてみましょう。
$y=x^2-2ax+3$($-1\leqq x\leqq 2$)の最小値を求めよ.
この問題の場合分けについて毎年色々と質問を受けるのですが、基本に忠実に考えていけば正しく理解できると思います。
とくに多いのが、場合分けの際のイコールをどのように付けたらいいのかという質問です。
とりあずグラフの概形を見たいので平方完成をして頂点を考えます。
$$y=(x-a)^2-a^2+3$$
となるので、軸は $x=a$ となります。ついでに $f(x)=(x-a)^2-a^2+3$ としておきましょう。
当然、$a$ の値によってグラフは動くことになるので、実際に動かして考えていくのが自然だと思います。
定義域 $-1\leqq x\leqq 2$ に対してグラフを横方向にスライドさせつつ、目で最小値の位置を確認していきます。
なるべく整理しながら考えたいので、定義域の右から左へとグラフを移動させていきましょう。もちろん左から右でもOKです。
大事なことは、最小値がどう表されるかということです。
まずはこんなグラフがイメージできます。
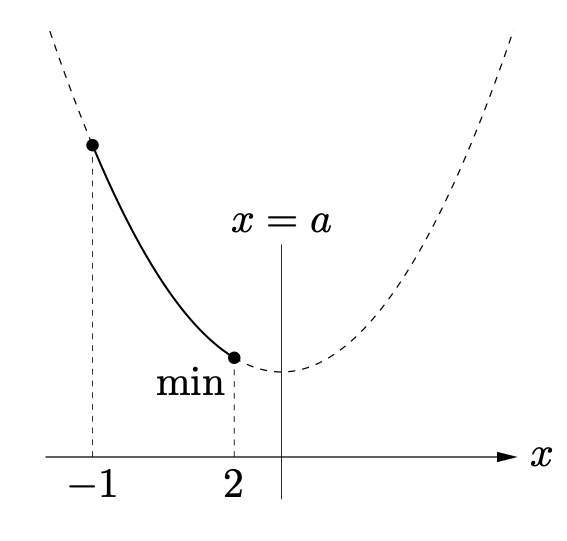
軸の位置:$a>2$
最小値は $x=2$ のときの値 $f(2)$
少しスライドさせてみましょう。
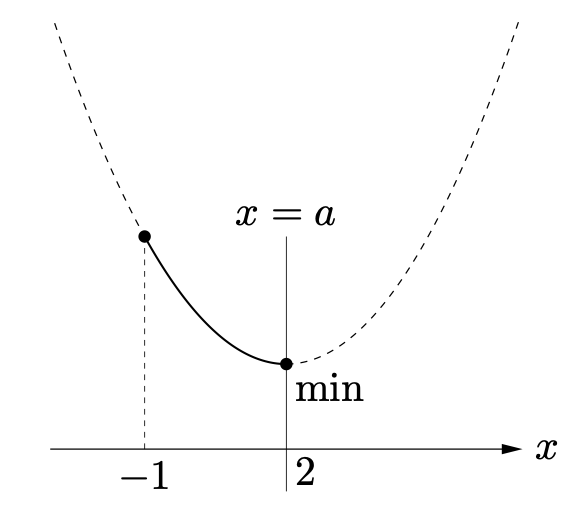
軸の位置:$a=2$
最小値は $x=2$ のときの値 $f(2)$
($x=a$ のとき $f(a)$ と表すこともできる)
もう少しスライドさせてみましょう。
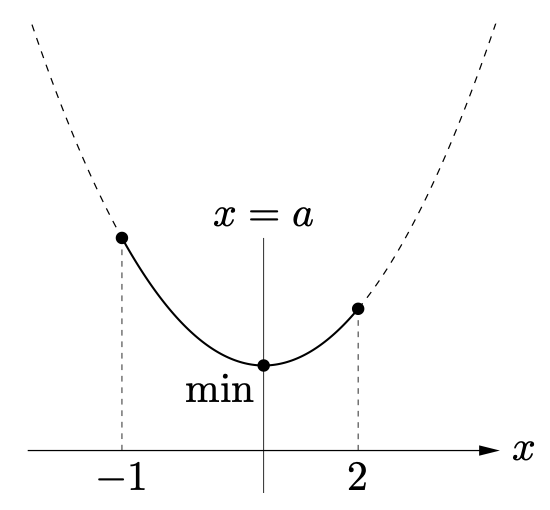
軸の位置:$-1<a<2$
最小値は $x=a$ のときの値 $f(a)$
ここから少し動かした、次の2つのグラフでも最小値は $f(a)$ となることを確認しましょう。
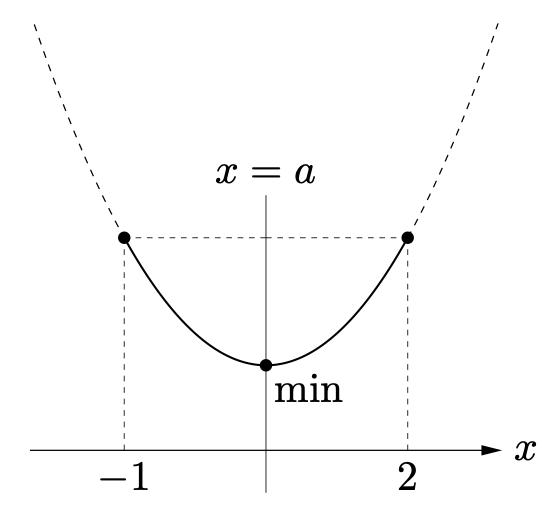
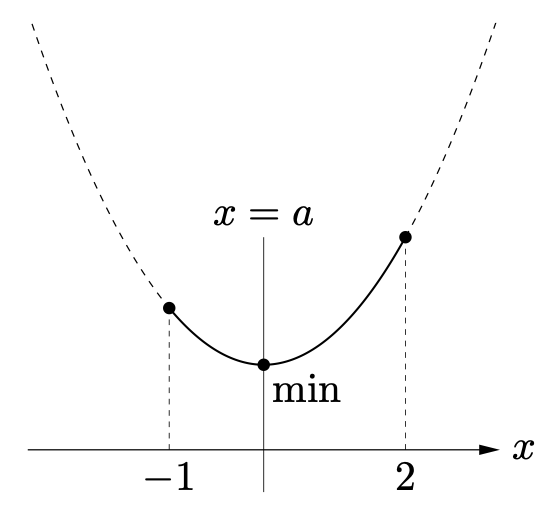
さらに少しスライドさせます。
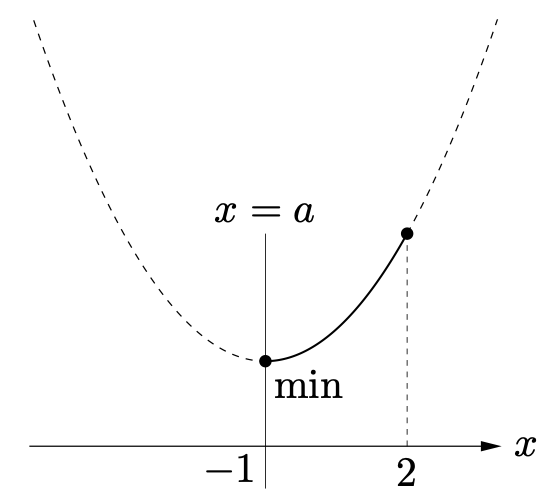
軸の位置:$a=-1$
最小値は $x=-1$ のときの値 $f(-1)$
($x=a$ のとき $f(a)$ と表すこともできる)
そして、最後にもう1つ確認しましょう。
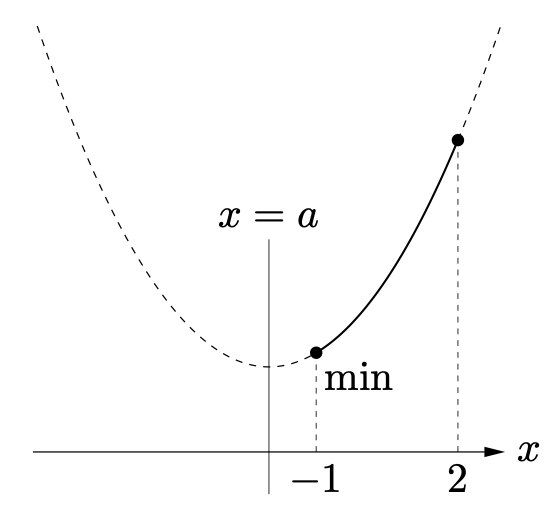
軸の位置:$a<-1$
最小値は $x=-1$ のときの値 $f(-1)$
というわけで、こうやっていろいろ書いてみると、結局最小値は $f(2)$ か $f(a)$ か $f(-1)$ かのいずれかで表されることが分かります。
したがって、最小値の表し方によって場合を分けます。
| 最小値 | どんな場合か |
| $f(2)$ | $a>2$ のときと $a=2$ のとき |
| $f(a)$ | $-1<a<2$ のときと $a=2$ のときと $a=-1$ のとき |
| $f(-1)$ | $a<-1$ のときと $a=-1$ のとき |
というわけで、綺麗にまとめていけば
$a\geqq2$ のとき、$f(2)=7-4a$
$-1\leqq a\leqq 2$ のとき、$f(a)=-a^2+3$
$a\leqq-1$ のとき、$f(-1)=4+2a$
のように書けるでしょう。
こうして見ていけば、場合分けのイコールをどうするかも簡単に分かります。
定義域の端点と軸が重なる場合は、2通りの表し方ができるので、どちらに入れてもいいのです。もちろん、両方に入れてもいいです。
1つずつグラフをかいて考えていけば、当たり前の話なのですが、どうもおかしなことを考えている生徒が多いようです。
気になって調べてみると、やはりおかしなことが書いてあります。
最小値は関数 $y=f(x)$ のグラフは下に凸であるから、軸が区間に含まれているときと含まれないとき、更に含まれないときは区間の左外か右外かで場合分けする。
こんなことが、問題集のポイントのようなところに書いてあるせいで、軸のことだけを考えて場合分けをしてしまう人が増えるのでしょう。
もちろん、場合を分けるのは軸の位置によりますが、その必要性は最小値がどう表されるかということから生じるものです。
その部分を考えないせいで、うまく場合分けができないという人が続出するようです。
大切なのは、まず自分の手でいろいろとグラフをかいてみること、そしてそのときの最小値はどう表されるかを考えてみることです。
最大値の話も同様に考えられます。
グラフがいろいろと変わっても、同じように考えば問題なくできるはずです。
どう解くかの話ばかりで、どう考えるか、どう考えられるべきかという話がすっぽり抜けてしまっている人が多すぎる気がします。












