関数のグラフの平行移動の話

塾長

もう梅雨が明けたような真夏の感じがやってきています。個人的には最高の気候です。浮かれちゃう！

現在、高校1年生は二次関数のあたりをやっています。

二次関数の内容は高校数学でも非常に重要となる内容なので、ここできちんと理解を深めておくことが大切です。

が、やはり何となく公式的なものを覚えておしまいみたいな感じで進んでしまっている人もたくさんいるようです。

この二次関数の単元では、グラフの平行移動や最大・最小、方程式や不等式への応用といった、今後にもつながる重要な内容がテンコ盛りなので、1つ1つの内容をじっくりと掘り下げて考えてみてほしいところです。

悩める
生徒

なんで $x$ 軸方に $\alpha$ 動かすのにマイナスがつくんですか？

このような質問を持ってくる生徒は、なぜそういう関係が成り立つのかを全く理解しておらず、結果だけを暗記してしまっています。

結果を暗記するのは数学の勉強ではありません。なぜそうなるかを考えることが数学の勉強の大事な部分です。

そんなに難しい話ではありません。少し考えてみましょう。

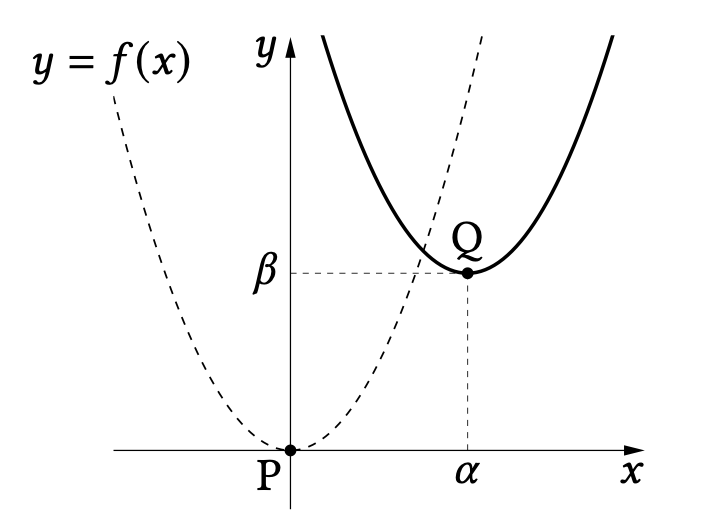
破線のグラフ $y=f(x)$ 上の点 $\mathrm{P}$ を $x$ 軸方向に $\alpha$、$y$ 軸方向に $\beta$ 移動した点を $\mathrm{Q}$ とします。

分かりやすく原点にしていますが、実際はグラフ上のすべての点が同様に動くのでどの点で考えても同じです。

なので、$\mathrm{P}(x,\ y)$、$\mathrm{Q}(X,\ Y)$ と一般化しておきましょう。

ここで、点 $\mathrm{P}$ を $x$軸方向に$\alpha$、$y$軸方向に$\beta$ 移動して点 $\mathrm{Q}$ をとります。あくまで点の移動だけ考えてください。

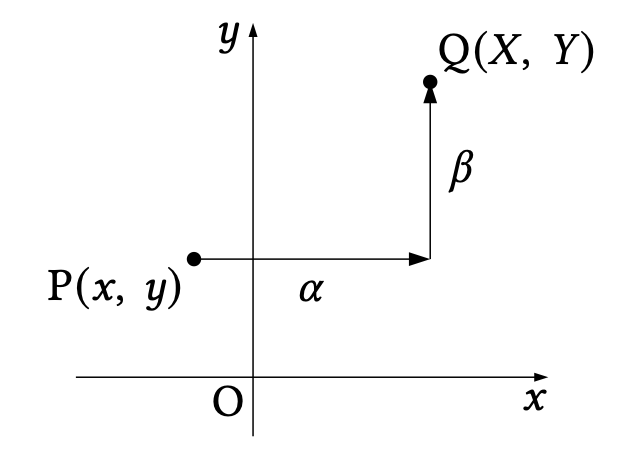
このとき、$(x,\ y)$ と $(X,\ Y)$ には次のような関係が成り立ちます。

\begin{align*}
\begin{cases}
X=x+\alpha\\
Y=y+\beta
\end{cases}
\end{align*}

が成り立ちます。これを書き直すと

\begin{align*}
\begin{cases}
x=X-\alpha\\
y=Y-\beta
\end{cases}
\end{align*}

です。また、$x$ と $y$ の間には、$y=f(x)$ という関係が成り立っています。

したがって、上の式を放り込めば

\begin{align}
Y-\beta=f(X-\alpha)
\end{align}

となります。これが移動先のグラフ上の点 $(X,\ Y)$ が満たす関係となります。

このままでも良いのですが、一般的には関数は小文字の $x$、$y$ を用いて表すので、小文字で表現すると

$$y-\beta=f(x-\alpha)$$

となります。

塾長

授業ではもう少し細かな点まで説明をしますが、こんな感じで確認をしています。

もちろん同じ内容が教科書にも書かれていますし、ちゃんとした学校であれば授業でも必ずやっているはずです。

こうした話をまずはザックリでいいので、自分の手で再現してみることが大切です。

問題集をやるのもいいですが、その前に教科書内容を正しく理解しているかどうかを確認してみてください。

こうした確認をするのとしないのとでは、大きな差が生まれます。日常の学習においても、ぜひ気を付けてみてください。