2025年度第5回石川県総合模試の数学を解いてみた(ダイジェスト版)

石川県総合模試を受験された皆さん、お疲れ様でした。今更感がありますが、第5回総合模試の解説記事です。
統一テストの直前ということもあり、第5回は受験者も増えることが多く、よりリアルな現在地を知ることができる模試と言えるでしょう。前回同様、基礎固めに力を入れてきた人は、そろそろ結果につながってくる時期です。また、ここからはより実戦的な入試の準備に取り掛かっていくことになります。今回の模試と、統一テストの結果をしっかりと分析して、今後の勉強に活用していきましょう!
概観
今回の数学のセットを解いてみた結果、全体的な難易度は「標準」と評価します。
大問1の小問集合から、資料の整理、関数、方程式、作図、平面図形、空間図形まで、全分野がバランス良く出題されました。過去の模試と同様に、「難問・奇問」のような問題はありませんでしたが、大問3(3)の関数と図形の融合問題、大問5の作図など、一部に「やや難」と言える問題が含まれていました。ここで点差がついたのではないかと思います。
いつもお伝えしていることですが、「試験時間内に全ての問題を解き切るのはかなり難しい」構成です。解けなかった問題がいくつかあったからといって、必要以上に気にしなくても大丈夫です。
重要なのは、普段から試験の対策ではなくちゃんと数学の勉強をすることです。正攻法で数学を学んでいれば、本番でもしっかり得点できる良問が揃っていました。
この記事を読み、復習の際はできなかった問題は時間を気にせずに取り組んでみてください。復習をやることで実力アップが期待できる良問が多いため、早めに復習をやっておきましょう。また、試験の反省と自己分析をきちんと行い、今後の学習に活かしていきましょう。
全体的な難易度標準
大問1:小問集合
難易度易
(1)はオの $\displaystyle \sqrt{98}-\frac{6\sqrt{6}}{\sqrt{27}}$ がポイントです。
$\sqrt{98}=\sqrt{49\times 2}=7\sqrt{2}$ くらいは暗算で計算したいですね。$\sqrt{27}=3\sqrt{3}$ も同様です。つまり $\displaystyle \frac{6\sqrt{6}}{\sqrt{27}}$ は $\displaystyle \frac{6\sqrt{6}}{3\sqrt{3}}$ と見て $2\sqrt{2}$ と計算できれば深く理解できていると言えます。
有理化しても良いですが、$\displaystyle \sqrt{\frac{6}{3}} = \sqrt{2}$ とした方が速いです。
(3)は、$60\times 30=xy$ がすぐに思い浮かべばOKです。
(4)は少し珍しい問題でしたが、内容はとてもシンプルです。きちんと定理の証明などを理解できていれば、難なくできたでしょう。
命題「$\mathrm{P}$ならば$\mathrm{Q}$」の逆は「$\mathrm{Q}$ならば$\mathrm{P}$」です。逆が成り立たないものを探すと良いでしょう。反例(成り立たない具体例)が1つでもあれば、その命題は成り立ちません。
- アの逆:対応する角の大きさが等しければ、2つの三角形は合同である。
偽(相似なだけで、合同とは限らない) - イの逆:二等辺三角形ならば、2つの角の大きさは等しい。
- ウの逆:1組の向かい合う角が等しい四角形ならば、平行四辺形である。
偽(もう1組の向かい合う角も等しくなければ、平行四辺形の条件を満たさない) - エ (逆):$\triangle \mathrm{ABC}=\triangle \mathrm{A}^{\prime}\mathrm{BC}$ ならば、$\ell // m$ である。
大問2:資料の整理
難易度標準
(1)では図1のヒストグラム(A組の生徒40人)から、箱ひげ図の作成に必要な5つの値(最小値、第1四分位数、中央値、第3四分位数、最大値)を読み取ります。
- 最小値 (min): 0冊の生徒が1人いるので、0冊。
- 最大値 (max): 9冊の生徒が2人いるので、9冊。
- 中央値 ($\mathrm{Q}2$): 40人の $\displaystyle \frac{1}{2}$、つまり20番目と21番目の生徒の平均値。
- 0冊 (1人) $\to$ 1人
- 1冊 (4人) $\to$ 累積 5人
- 2冊 (2人) $\to$ 累積 7人
- 3冊 (5人) $\to$ 累積 12人
- 4冊 (4人) $\to$ 累積 16人
- 5冊 (9人) $\to$ 累積 25人
- 20番目と21番目の生徒は、両方とも「5冊」の階級にいます。よって $\mathrm{Q}2$ = 5冊。
- 第1四分位数 ($\mathrm{Q}1$): 40人の $\displaystyle \frac{1}{4}$、つまり10番目と11番目の生徒の平均値。
- 累積7人の次、10番目と11番目は「3冊」の階級にいます。よって $\mathrm{Q}1$ = 3冊。
- 第3四分位数 ($\mathrm{Q}3$): 40人の $\displaystyle \frac{3}{4}$、つまり30番目と31番目の生徒の平均値。
- 累積25人の次、6冊の階級は5人(累積30人)、7冊の階級は4人です。
- したがって、30番目の生徒は「6冊」、31番目の生徒は「7冊」です。
- $\mathrm{Q}3 = \displaystyle \frac{6+7}{2} = $ 6.5冊。
この5つの値(最小値0, $\mathrm{Q}1=3$, $\mathrm{Q}2=5$, $\mathrm{Q}3=6.5$, 最大値9)と一致する箱ひげ図は「ウ」です。
(2)は散らばりぐあいの比較を記述する問題でした。出題される頻度の低い問題だったので戸惑った人もいたかもしれません。
データの「散らばりぐあい」を比較するには、(1)データ全体の幅である「範囲」(最大値-最小値)と、(2)データの中央50%の幅である「四分位範囲」($\mathrm{Q}3$-$\mathrm{Q}1$)の2つを見るのが基本です。
A組、B組、C組のそれぞれの値を、図1と図2から読み取って比較表を作成します。
| 組 | 最小値 | Q1 | Q2 | Q3 | 最大値 | 範囲 (Max−Min) | 四分位範囲 (Q3−Q1) |
| A組 | 0 | 3 | 5 | 6.5 | 9 | 9 | 3.5 |
| B組 | 0 | 3 | 6 | 7 | 10 | 10 | 4 |
| C組 | 1 | 3.5 | 5 | 7 | 10 | 9 | 3.5 |
上記の表から、B組は「範囲」(10冊)が3組の中で最も大きく、また「四分位範囲」(4冊)も3組の中で最も大きいことがわかります。この2つの指標がどちらも最大であることから、データの散らばりぐあいが最も大きい組はB組であると判断できます。
大問3:2次関数(復習おすすめNo.2)
難易度標準
(1)は $y$ の変域を求める基本的な問題でした。これはグラフを描いて考えれば問題ないでしょう。
(2)は $\triangle \mathrm{APB}$ の面積を求める問題でした。
まず、各点の座標を求めます。$\mathrm{A}(-2,\ 2)$、$\mathrm{B}(4,\ 8)$、$\mathrm{P}(2,\ 2)$ はサッと計算して出しておきましょう。
ここで図を見てみましょう。$\triangle \mathrm{APB}$ の辺$\mathrm{AP}$は $y=2$ の高さにあり、$x$ 軸と平行です。
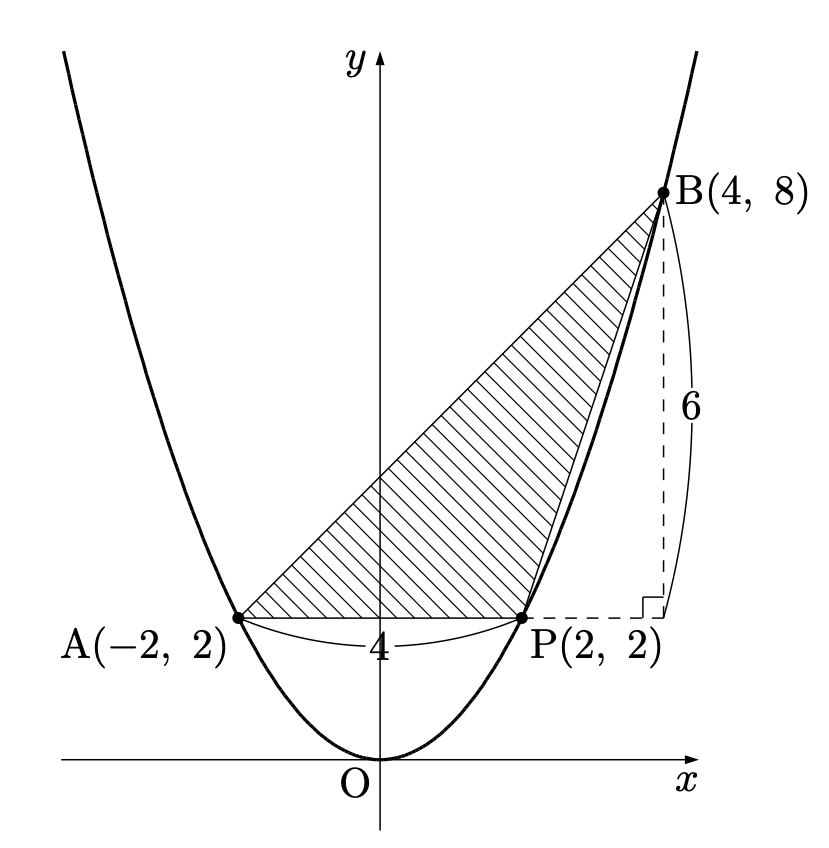
このように $x$ 軸や $y$ 軸に平行な辺がある場合、面積計算は非常に簡単になります。
$\triangle \mathrm{APB}$ の底辺は $\mathrm{AP}=4$、高さは点 $\mathrm{B}$ との $y$ 座標の差を考えて $6$ となります。したがって
$$\frac{1}{2} \times 4 \times 6 = 12$$
辺$\mathrm{AP}$を底辺とみなします。
(3) は面積の条件から直線 $\mathrm{BP}$ の式を考える問題でした。
まず条件 $\triangle \mathrm{APR} = \triangle \mathrm{BQR}$ を言い換えることが重要です。
$\mathrm{R}$ は $\mathrm{AB}$ と $\mathrm{PQ}$ の交点です。
$\triangle \mathrm{APQ}$ という三角形を考えると、これは $\mathrm{R}$ によって $\triangle \mathrm{APR}$ と $\triangle \mathrm{ARQ}$ に分割されます ($\triangle \mathrm{APQ} = \triangle \mathrm{APR} + \triangle \mathrm{ARQ}$)。
同様に、$\triangle \mathrm{ABQ}$ という三角形は $\triangle \mathrm{BQR}$ と $\triangle \mathrm{ARQ}$ に分割されます ($\triangle \mathrm{ABQ} = \triangle \mathrm{BQR} + \triangle \mathrm{ARQ}$)。
$\triangle \mathrm{ARQ}$ は共通部分です。
したがって、$\triangle \mathrm{APR} = \triangle \mathrm{BQR}$ が成り立つとき、$\triangle \mathrm{APQ} = \triangle \mathrm{ABQ}$ も成り立ちます。

ここで、$\triangle \mathrm{APQ}$ と $\triangle \mathrm{ABQ}$ を図で見てみましょう。この2つの三角形は、辺 $\mathrm{AQ}$ を共通の底辺としています。
共通の底辺 $\mathrm{AQ}$ を持つ2つの三角形の面積が等しいということは、残りの頂点 $\mathrm{P}$ と $\mathrm{B}$ が、底辺 $\mathrm{AQ}$ から等しい距離にある、すなわち $\mathrm{PB} // \mathrm{AQ}$ であることを意味します。
この「傾きが等しい」という条件さえ導ければ、あとは計算るのみです。
直線 $\mathrm{AQ}$ の傾き は
$$\frac{\displaystyle \frac{25}{2} - 2}{5 - (-2)} = \displaystyle \frac{\displaystyle \frac{21}{2}}{7} = \displaystyle \frac{3}{2}$$
求める直線 $\mathrm{BP}$ の傾きも $\displaystyle \frac{3}{2}$ です。
直線 $\mathrm{BP}$ の式を $y = \displaystyle \frac{3}{2}x + b$ とおき、点 $\mathrm{B}(4, 8)$ を代入します。
$$8 = \displaystyle \frac{3}{2}\times 4+b$$
よって、$b=2$
よって、求める式は $y = \displaystyle \frac{3}{2}x + 2$ です。
大問4・連立方程式
難易度標準
まず、A組の生徒数を $x$ 人、B組の生徒数を $y$ 人とおきます。
テスト当日の人数が同じだったので、$x-3 = y-1$。
これを変形し $y = x-2$ としておくと、B組の人数 $y$ を $x$ で表せるため、1元1次方程式として解くことができます。
次に「平均点」の定義、すなわち「合計点 $\div$ 人数」をもとに考えていきます。
- A組の合計点: $62.4x$
- B組の合計点: $58.5y = 58.5(x-2)$
- A組B組全員の人数: $x+y = x + (x-2) = 2x-2$
- A組B組全員の平均点: $60.5$ 点
- A組B組全員の合計点: $60.5(x+y) = 60.5(2x-2)$
「A組合計 + B組合計 = 全員合計」なので、
$$62.4x + 58.5(x-2) = 60.5(2x-2)$$
この方程式を解けばA組が $x=40$ 人となり、B組は $x-2 = 40-2 = 38$ 人となります。
大問5・作図(復習おすすめNo.3)
難易度やや難
まずは、条件を満たすような図をざっくりと描いてみましょう。
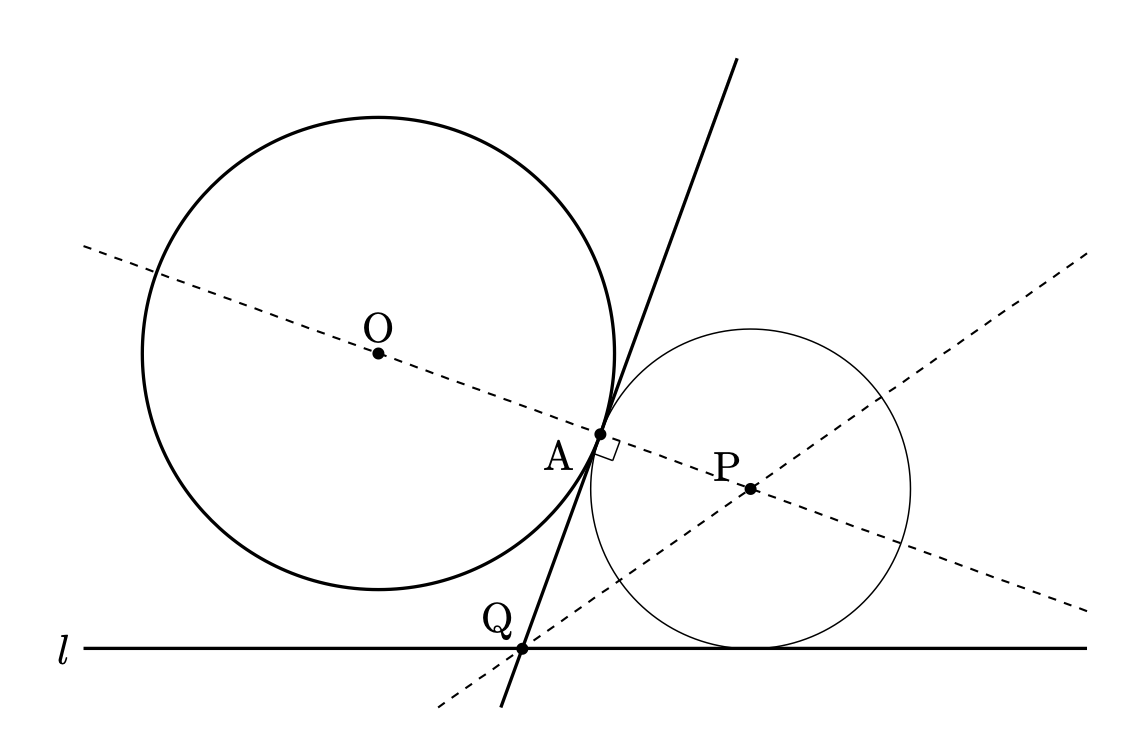
この図と与えられた条件を比べながら、どのように作図をしていくべきかを考えます。
- 条件1: 点$\mathrm{P}$は、円$\mathrm{O}$の外部にある。
- 条件2: $\mathrm{P}$ を中心とする円は「点 $\mathrm{A}$ を通る円 $\mathrm{O}$ の接線」(これを $t$ とします)と点 $\mathrm{A}$ で接する。
- 円 $\mathrm{P}$(中心 $\mathrm{P}$)が $t$ と点 $\mathrm{A}$ で接するので、半径 $\mathrm{PA} $は接線 $t$ と垂直($\mathrm{PA} \perp t$)である。
- 一方、接線 $t$ は円 $\mathrm{O}$ の接線でもあるので、半径 $\mathrm{OA}$ とも垂直($\mathrm{OA} \perp t$)である。
- $\mathrm{PA} \perp t$ かつ $\mathrm{OA} \perp t$ であり、どちらも点 $\mathrm{A}$ を通るので、$\mathrm{P}, \mathrm{A}, \mathrm{O}$ の3点は同一直線上にあることになります。
- 条件3: $\mathrm{P}$ を中心とする円は、直線 $l$ と接する。
- 条件4: $\mathrm{P}$ を中心とする円は点 $\mathrm{A}$ を通るので、円 $\mathrm{P}$ の半径は $\mathrm{PA}$ の長さに等しい。
条件2を言い換えると、点 $\mathrm{P} $は、直線 $\mathrm{OA}$ 上にあると言えます。条件3を言い換えると、$\mathrm{P}$ から直線 $l$ までの距離が、円 $\mathrm{P}$ の半径と等しいと言えます。条件4を言い換えると、円$\mathrm{P}$の半径 = $\mathrm{PA}$ となります。
以上から、$\mathrm{PA}$ の長さと $\mathrm{P}$ から直線 $l$ までの距離は等しくなければなりません。
ここで、(A)の「$\mathrm{P}$は直線$\mathrm{OA}$上にある」ことと、接線 $t$ が $\mathrm{OA} \perp t$ であることを思い出します。
点$\mathrm{P}$(直線$\mathrm{OA}$上)から接線 $t$ までの距離は、$\mathrm{PA}$ の長さに一致します。
つまり、条件は「$\mathrm{P}$ から $t$ までの距離」=「$\mathrm{P}$ から $l$ までの距離」と書き換えられます。2直線 $t$ と $l$ から等しい距離にある点の集まりは、その2直線のなす角の二等分線となります。
これは最初にざっくり描いた図からも予想できます。
したがって、求める点$\mathrm{P}$は、「直線$\mathrm{OA}$」と「接線 $t$ と直線 $l$ のなす角の二等分線」との交点ということになります。
大問6・平面図形
難易度標準(本当は易に分類したいくらいのレベルの問題でした)
(1)は角度を求める単純な問題でした。
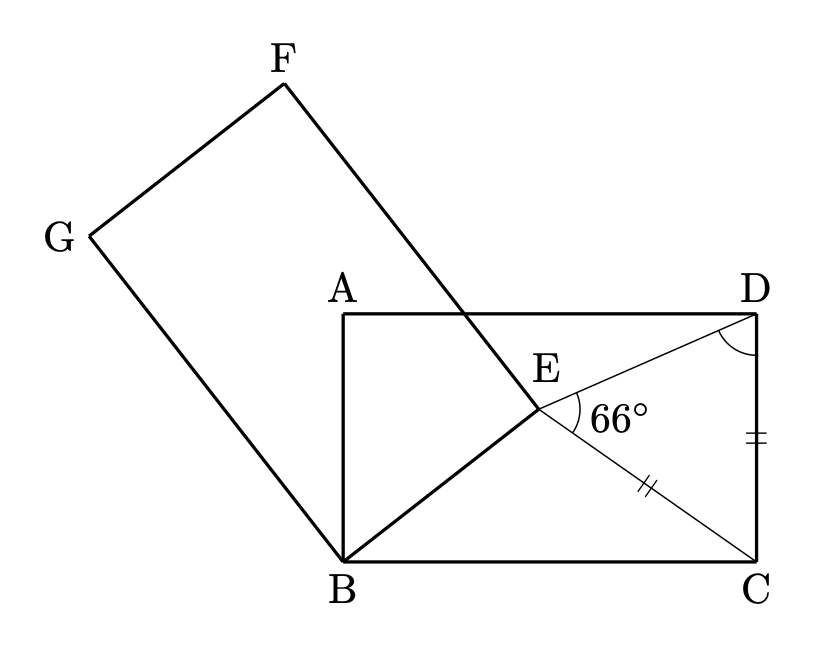
$\triangle \mathrm{CDE}$ に着目します。条件より $\mathrm{CE} = \mathrm{CD}$ なので、$\triangle \mathrm{CDE}$ は二等辺三角形です。よって
$$\angle \mathrm{DCE} = 180^{\circ} - 66^{\circ}\times 2 = 48^{\circ}$$
となります。
(2)も合同の証明という定番中の定番問題でした。$\triangle \mathrm{ABG} \equiv \triangle \mathrm{EBC}$ を示す問題です。
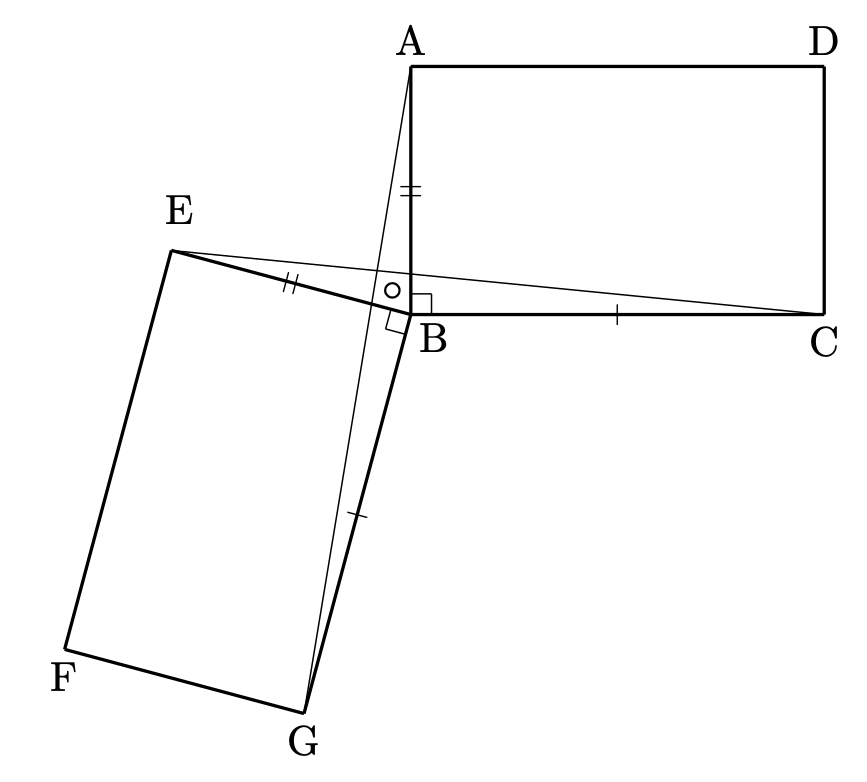
仮定からすぐに、$\mathrm{AB} = \mathrm{EB}$、$\mathrm{BG} = \mathrm{BC}$ が分かります。
となれば、狙っていくのは $\angle \mathrm{ABG} = \angle \mathrm{EBC}$ でしょう。
長方形の内角は $90^{\circ}$ なので、$\angle \mathrm{ABC} = 90^{\circ}$、$\angle \mathrm{EBG} = 90^{\circ}$ であることから
$$\angle \mathrm{ABG} = \angle \mathrm{ABE} + \angle \mathrm{EBG} = \angle \mathrm{ABE} + 90^{\circ}$$
$$\angle \mathrm{EBC} = \angle \mathrm{ABE} + \angle \mathrm{ABC} = \angle \mathrm{ABE} + 90^{\circ}$$
が言えます。したがって、$\angle \mathrm{ABG} = \angle \mathrm{EBC}$ となるので
$$\triangle \mathrm{ABG} \equiv \triangle \mathrm{EBC}$$
(3)は線分比の問題でしたが、何ということもない問題でした。
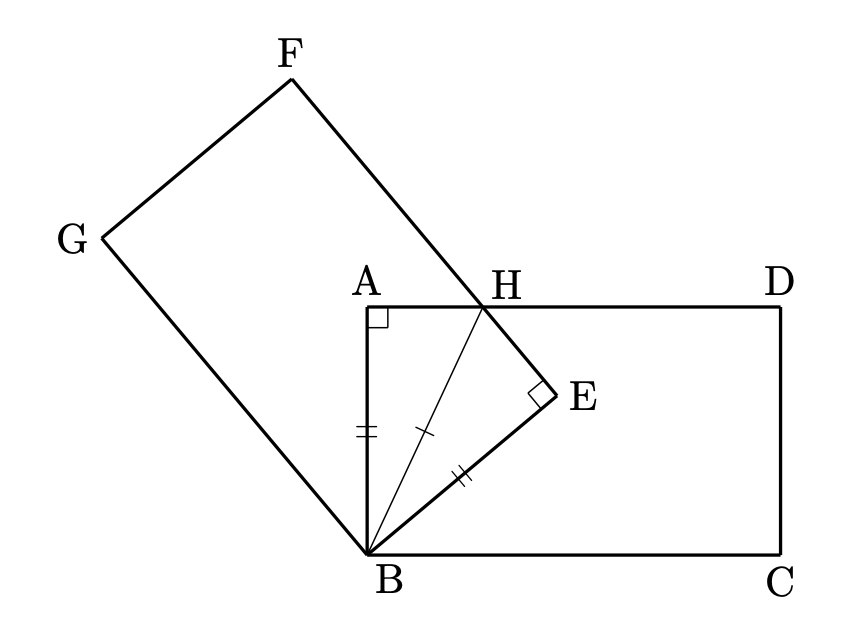
図において、四角形 $\mathrm{ABEH}$ の面積が四角形 $\mathrm{BCDH}$ の面積の $\displaystyle \frac{4}{11}$ 倍になるときの $\mathrm{AH}$ の長さを求める問題です。
まず、図にも示したように、2つの直角三角形 $\triangle \mathrm{ABH}$ と $\triangle \mathrm{EBH}$ の合同はすぐに見抜けなければなりません。
この合同から、四角形 $\mathrm{ABEH}$ の半分が $\triangle \mathrm{ABH}$ の面積となります。
すなわち、$\triangle \mathrm{ABH}$ の面積は四角形 $\mathrm{BCDH}$ の面積の $\displaystyle \frac{2}{11}$ となります。すなわち面積比は $2:11$ となります(下図)。
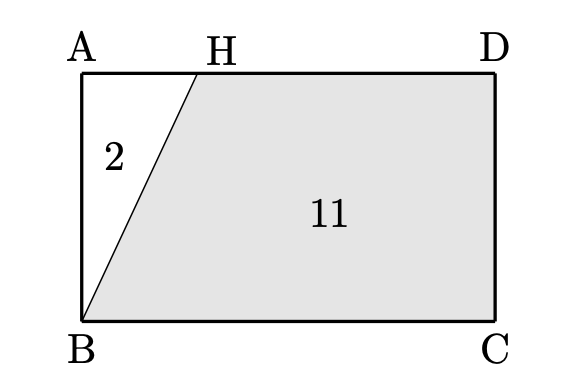
ここからすぐに $\mathrm{AH:HD}=4:9$ と求められるようになっておきたいところです。求められない人は、下の図を見てよく考えてみてください。

こういうところで無駄な計算をしてしまう人が多いので気をつけましょう。図を活用して計算は最低限になるように!
大問7・空間図形(復習おすすめNo.1)
難易度標準
(1)はもはや解説不要でしょう。
(2)は四角錐 $\mathrm{A}-\mathrm{BCQP}$の体積を求める問題でした。
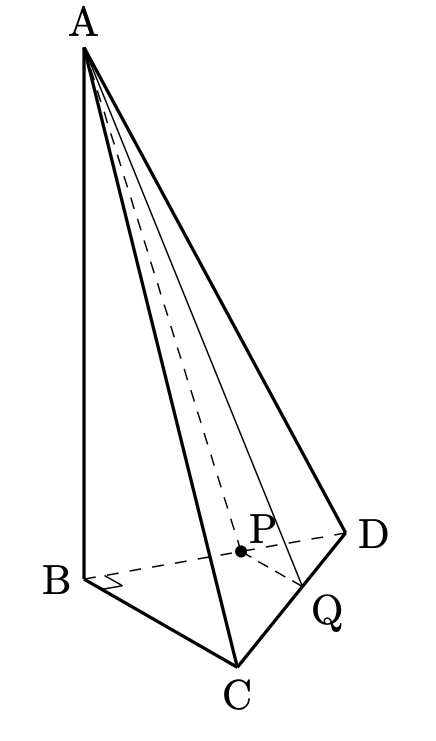
高さは $\mathrm{AB=10}$ がそのまま使えるので、底面積を考えればOKです。
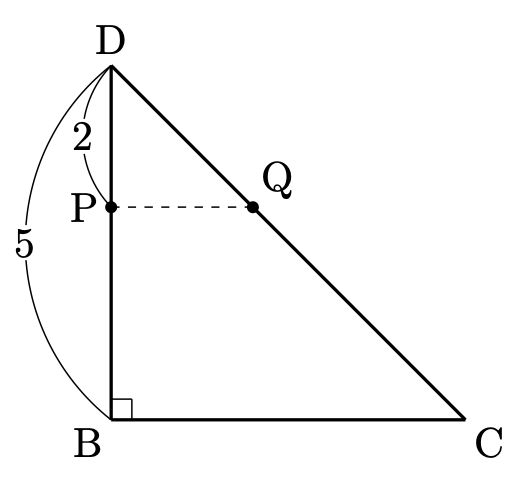
底面は $\triangle \mathrm{PQD}$ と $\triangle \mathrm{BCD}$ の相似を利用します。相似比は図からすぐに $2:5$ とわかります。したがって、面積比は
$$\triangle \mathrm{PQD}:\triangle \mathrm{BCD}=4:25$$
四角形 $\mathrm{BCQP}$ は $25-4=21$ であることから、さらに
$$\triangle \mathrm{BCD}:\mathrm{BCQP}=25:21$$
ここで、三角錐$\mathrm{A}-\mathrm{BCD}$ の体積 $V$ は
$$V =\frac{1}{3} \times \frac{25}{2} \times 10 = \frac{125}{3}$$
底面積の比がそのまま体積比となるので、求める立体の体積は
$$\frac{125}{3}\times \frac{21}{25}=35$$
となります。
(3)は線分の長さを求める問題でした。
展開図から考える問題で、ここは少々面食らった人もいたかもしれないですね!
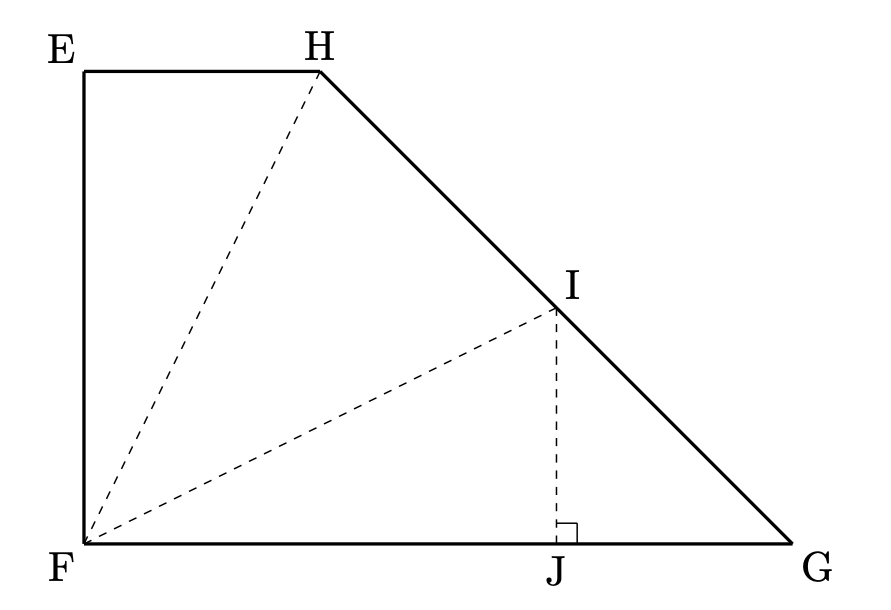
まずは、展開図を組み立てて、頂点を確定させておきましょう。
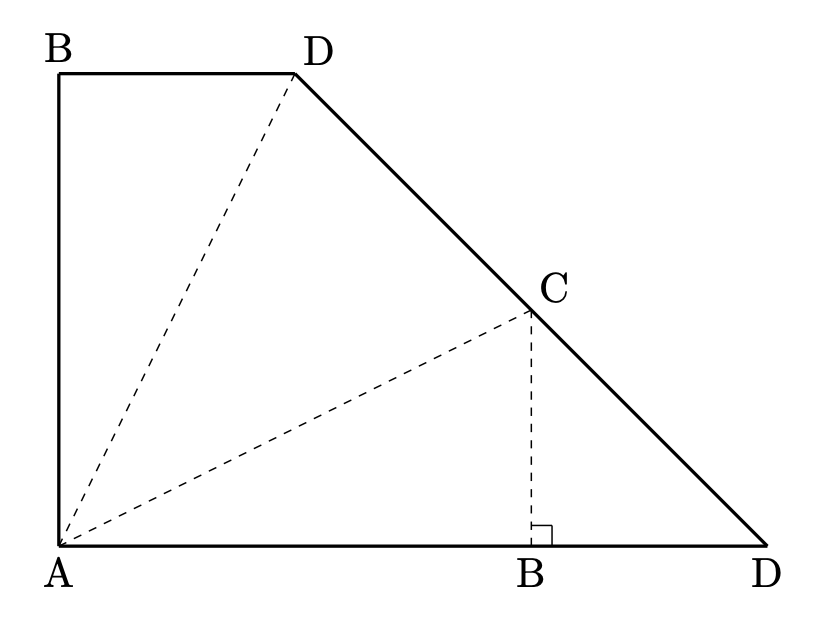
頭の中で組み立てられない人は、紙を切って実際に組み立ててみてください!
この問題は、入試の空間図形定番の体積を2通りの方法で表して高さを求める考え方を使います。
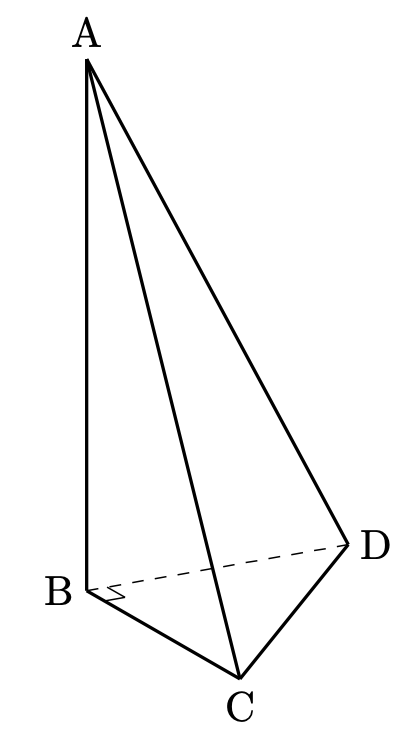
$\mathrm{BI}$は、三角錐を頂点$\mathrm{B}$、底面$\mathrm{ACD}$」として見たときの「高さ」となります。ちなみに、この三角錐の体積は(2)で計算したように $V = \displaystyle \frac{125}{3}$ です。
まずは、$\triangle \mathrm{ACD}$ を求めていきましょう。これは、図から $\mathrm{DC=CD}$ が瞬時に分かるので、$\triangle\mathrm{ADC}$ を求めればOKとわかります。
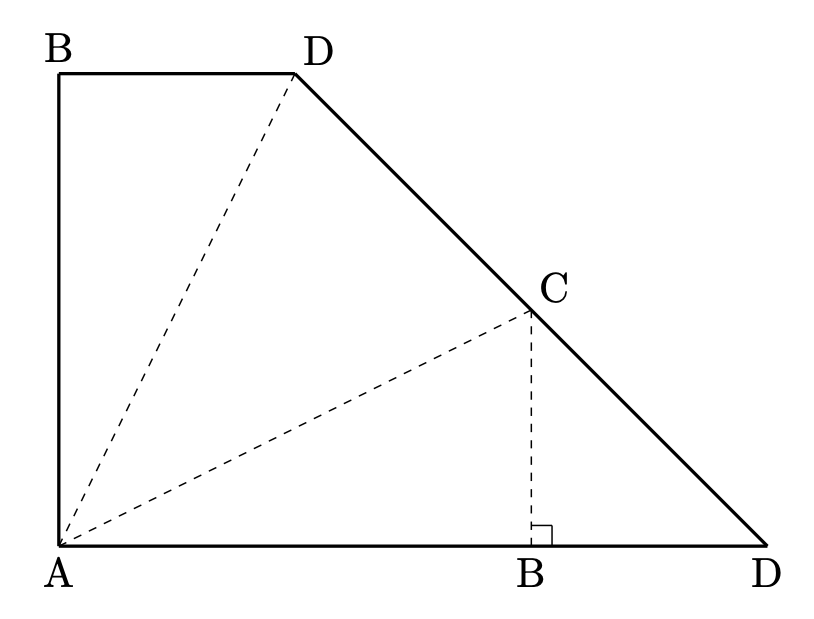
$$\triangle\mathrm{ADC}=\frac{1}{2}\times 15\times5=\frac{75}{2}$$
よって、$\displaystyle\triangle\mathrm{ACD}=\frac{75}{2}$ となります。
したがって、
$$\frac{125}{3} = \frac{1}{3} \times \frac{75}{2} \times \mathrm{BI}$$
$$\frac{125}{3} = \frac{1}{3} \times \frac{75}{2} \times \mathrm{BI}$$
$\displaystyle125 = \frac{75}{2} \times \mathrm{BI}$ より、
$$\displaystyle \mathrm{BI} = \frac{10}{3}$$
まとめ
今回の模試は、1つ1つの問題を取り上げると、作図以外で難しい問題は1つもありませんでした。解くのに要した時間は、20分あるかないかといった感じでした。個人的に統計が嫌いすぎて大問2で時間がかかりました笑。
後半の図形は、作図が中学生には厳しいレベルだなあと思いましたが、平面図形・空間図形ともに、よくあるタイプの問題で構成されていて、難しさもそこまで高くなく、サクサク解けた人もいたでしょう。
高得点者がいる一方で、苦手な人・準備不足の人はあまり得点できないような問題が多く、実力が反映されやすいレベルのテストだったのではないかと思います。
上位校狙いの人で、今回あまり得点できなかったという人は、普段の数学の勉強の進め方を再点検すべき時期にきています。時間をかけている割に目標とするラインまで到達していない人は、もしかするとおかしな方向に進んでしまっている可能性があるので注意しましょう。
というわけで、11月は模試と統一テストが連続して実施されました。志望校を決定する上でも重要と言われますが、まだまだこの時期の成績は当てになりません。今回、悔しい思いをした人もこれからの勉強次第で大きく飛躍できます。
自分が行きたい高校があるのであれば、合格を目指して全力で頑張りましょう!


