石川県公立高校入試の数学を解いてみた

ここ数日は、国公立前期の発表と公立高校入試でドタバタしておりました。まだ、ドタバタしていますが、取り急ぎ数学のネタを投下しておきます(笑)
解答などはすでに新聞にも載っていたので確認された方も多いかなと思います。
概観
大問数7・小問数22ということで、石川県総合模試などに比べると問題数は若干少ない構成でした。
大問順に見ると、小問集合、規則性、関数、方程式、作図、平面図形、空間図形という the 公立高校入試といった感じの出題でしたね。どの問題も数学の問題として見ると標準的なレベルでしたが、余計な情報が入り込んでいて、面倒だなと感じた生徒も多かったかもしれません。水道料金やドーナツとカップケーキの販売など、日常的なものと数学を関連させた問題が含まれており、こうした傾向は大学入試改革の影響を受けているのでしょう。こうした部分で時間を取られてしまった人もいるかもしれません。
全体的には難問と言える問題はなく、比較的平易なテストだったのではないかと思います。上位校では高得点者も多そうなので、小さなミスが影響しそうな問題だと思います。
全体的な難易度やや易
以下では、各大問の概要と興味のある問題を取り上げてみたいと思います。
各問題の概要
大問1
内容小問集合
難易度易
前半は、単純な計算問題ばかりです。計算のルールや方法についてはしっかりと準備をして満点を狙いたい部分です。模試などの分析でも触れましたが、計算ミスが多い人は「計算過程をしっかり書け」と言われることが多いと思いますが、暗算力を高めることも大切です。とくに高校入試レベルの計算問題では、2行程度で終わらせられるように準備しておきたいところです。
(2)の2次方程式は解の公式を使うだけの問題です。このような「覚えておけば解ける」という問題を入試問題の中に入れるのは嫌いです。2次方程式の計算問題ではもう少し頭を使う問題を入れて欲しいなあと思います。
こんなのとかだと面白いんですけどね。方程式って何か?という根本を問う問題があってもいいと思います。
(3)もどこかで見たような問題です。例の表を作ってしまえば瞬殺です。
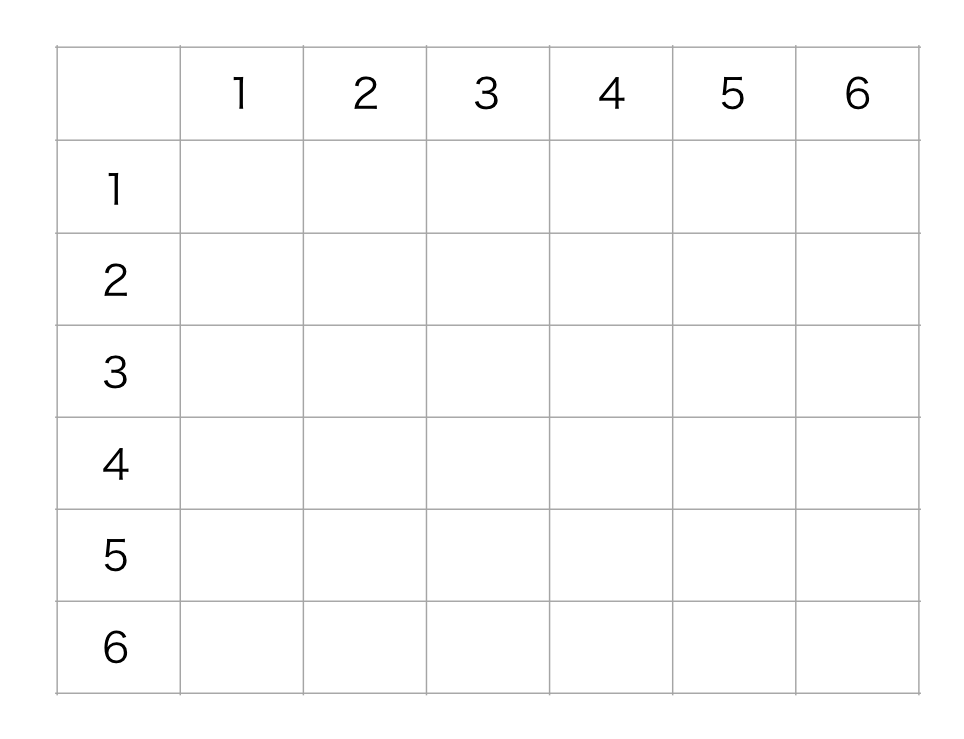
5の倍数なので、5の列と行を塗りつぶせば11個あることがすぐに発見できるでしょう。
(4)の関数の問題もグラフを思い描いて $y$ の動く範囲を考えれば問題ないでしょう。端点の $x=-1$ と $x=2$ を代入しただけで終わっている人は関数というものを根本から理解できていない可能性大です。高校入学までにきちんと復習しておきましょう!
大問1はサクっと終わらせたいのですが、ここを落とすと痛いので慎重にやったという人も多いかもしれません。素早く正確にというのは、数学のテストでは常に意識しておきたいですね。
大問2
内容規則性
難易度標準
今年の入試問題の中では、この問題がいちばん好みでした。いろいろな解き方ができるのですが、周期性に気づけたかどうかというのがポイントになります。
(1)は具体的にやってみれば、すぐに2秒後であることに気づくでしょう。
(2)もいくつか具体例を書き出して考えていけば、それほど難しくはありません。
| 秒 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 点P | A | C | E | A | C | E | A | C | E |
| 点Q | D | C | B | A | F | E | D | C | B |
上のように表にしてみると、PとQがともに周期性を持っていることが(当たり前ですが)わかります。そして、ともにCの位置に来る $n$ も周期的に現れることが分かります。本当はもう1周期分くらい書いてみるといいのですが、ここではスペースがないので割愛します。
1秒後、7秒後、13秒後、$\cdots$ となって現れるのが分かります。つまり、最初の1秒後の位置から、6秒ごとにPとQがCに位置することになります。これは $n$ が1増えると6秒経過するということです。また、Pは1秒で2m進むので、6秒では12m進むことも押さえましょう。つまり、$n$ が1増えるとPは12m進むわけです。
では $n=1$ 、つまり最初にCで出会う位置ををスタートにしてみると・・・
| $n$ | $1$ | $2$ | $3$ | $4$ |
| Pの進んだ距離 | 0 | 12 | 24 | 36 |
となるので、Pの進んだ距離は $12(n-1)$ として求められます。しかし、これでは最初にPがAからCへ進む2mが無視されているので、これを加えて、$12(n-1)+2=12n-10$ となります。
最初の2mは初期値であり、周期に入らない部分なので一旦無視して考えてみるのがいいでしょう。
高校入試の問題では、規則性の問題に面白い問題が多いです。数学が好きな人は、規則性の問題をいろいろとやってみるといいのではないかと思います。
大問3
内容関数
難易度易
関数は水道料金(従量課金)の問題でした。携帯電話の料金などもよく取り上げられますね。大切なことはグラフをかけることと、それを利用することです。高校入試レベルの関数の問題では情報を視覚化することが重要となります。
問題にごちゃごちゃと条件が書かれていたので難しいと思った人もいるかもしれませんが、数学的には非常に簡単な問題でした。こうした数学以外の部分で面倒な問題というが今後も増えることが予想されます。個人的にはあまり好きではありませんが、まあ仕方ないですね・・・。
さて、この問題はグラフが問題にかかれていたので非常に簡単でした。(1)は表を見て考えれば簡単です。(2)も単純に2点 $(20,\ 2200)$、$(30,\ 3700)$ を通るグラフから直線の式を求めるだけの問題です。
(3)の問題文を読みながら、私は正直「面倒くさいな」と思いました(笑)
ここでは冗長な問題文から必要な情報を取り出せたかどうかが鍵になります。大事なのは、基本料金700円と、使用料金は一定(単純な直線のグラフになる)であること、元のグラフの $20\mathrm{m}^2$ のときより高く $30\mathrm{m}^2$ のときより低いという点です。
つまりは、グラフで考えると下の2本の色付きの直線に挟まれるような直線であればOKということなんです。
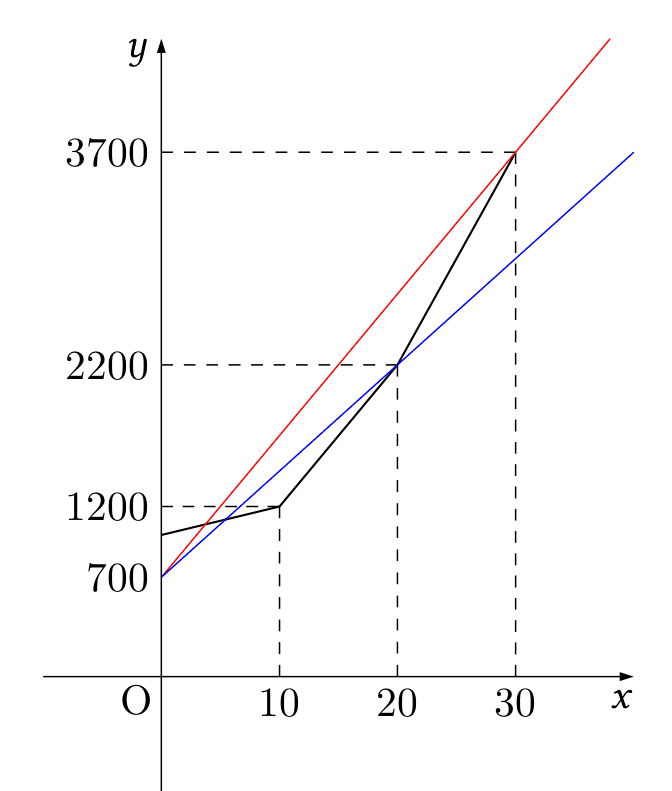
あとは、この2本の色付きの直線の傾きを求めればOKです。
大問4
内容方程式
難易度易
これも、入試対策をきちんとやってきた人にとっては朝飯前の問題だったと思います。ドーナツを $x$ 個、カップケーキを $y$ 個として、小麦粉と料金でそれぞれ方程式を立てればOKです。砂糖だとかバターだとかはフェイクです。
大問5
内容作図
難易度標準
作図は難しくもなく単純でもなく、ほどほどの問題でした。作図で基本になるのは等しい距離です。これを基本として、垂線や平行線がかけることを押さえておけば問題なくできたのではないでしょうか。
まず、$\mathrm{AP=CP}$ なのでPはACの垂直二等分線上に存在することが分かります。また、BPを直径とする円の周上に点Cがあることから、$\angle\mathrm{BCP}=90^{\circ}$ と言い換えられたかどうかがポイントです。 この2つを押さえればあとは簡単ですね!
作図の問題では、どう作図するかばかり考えてしまう人がいますが、まず大事なのは図形の知識です。とくに、同じ距離(長さ)というのはコンパスが威力を発揮する最大のポイントになります。
大問6
内容平面図形
難易度易
平行四辺形を題材としたオーソドックスな図形の問題でした。錯角や同位角をうまく利用しながら考えばそれほど難しくはない問題です。(3)も定番中の定番の最短距離の問題でした。最短距離は直線を考えますが、その際に対称性をうまく利用することがポイントになります。
平面図形の問題は、拍子抜けした人も多かったかもしれません。もう少し面白い性質などを題材にしてあれば良かったのですが、まあ、これは点取り問題ですね(笑)
大問7
内容空間図形
難易度易
空間図形も平面図形と同様に簡単でした。空間図形が圧倒的に苦手、という人でない限りは解けたのではないかと思います。ただし、計算がやや煩雑なので計算ミスをすると痛いですね。
(2)では図だけ見て長方形になると勘違いした人がいたかもしれません。雰囲気でやってしまうと痛い目を見ます。ここでは、条件から分かることは $\mathrm{CP=PE=EQ=QC}$ だけなので、ひし形ということしか分かりません。ひし形の面積は対角線をもとに2つの三角形に分ければOKです。
(3)も切断の問題ですが、これもよくあるタイプの問題です。2つの図形に割って体積を求めればOKです。
まとめ
途中から解説することもとくにないなあ(つまんね〜)と思ってしまいました。申し訳ありません(笑)
う〜ん、統一テストがなかなか面白かったので入試問題も期待をしていたのですが「流行りに乗っかった」という感じの問題が多く、内容的にはそこまで深い問題はありませんでしたね。
生徒の話を聞いた限りでは、数学で差をつけようと思っていた人にはちょっと厳しいかもしれません。どちらかというと英語の出来が影響しそうな感じですね。
何にしても、高校入試は終了です。受験生のみなさんお疲れ様でした!
点数が気になっている人、合否が気になっている人、いろいろいらっしゃるかもしれませんが、もう結果は変わりません。
やるべきことは反省と、次に向けた準備です。とくに数学はきちんとした準備をしておかないと高校入学後に苦労することになると思います。入試のストレスを発散したら、また高校へ向けての準備を始めましょうね!














