2025年度第8回石川県総合模試の数学を解いてみた

塾長

いよいよ公立高校入試前の最後の総合模試が実施されました。

最終回は毎年、私立受験や附属高の受験と時期が近く、受験者数がガクッと減るため当塾でも受験は任意としていますが、今年はどのくらいの受験者だったのでしょうか。

この時期の模試は、志望校判定というよりも、「本番でシミュレーション」としての意味合いが大きくなります。本番でどのように振る舞うかを、しっかりと確認できていればOKです。判定や点数はもう参考程度に考えて、間違えた問題の「原因」を突き止め、残り期間の学習計画に落とし込んでいくことを最優先しましょう。

概観

出題形式はいつも通りの大問7題構成でした。

全体的な難易度は「標準」ですが、今回は前半の代数分野と後半の幾何分野で難易度の差が大きく、とくに大問6の平面図形や大問7の空間図形では、複数の知識（相似、三平方の定理、円周角など）を組み合わせるやや難易度の高い問題がありました。計算量もそれなりにあるため、時間配分が鍵となったはずです。

上位校（泉丘・二水・桜丘）を目指す人は、大問1〜4までを「ノーミスかつハイスピード」で通過できたかがポイントです。ここで時間を使いすぎると、後半の図形問題で焦ってしまうことになるでしょう。前半で時間を節約し、後半の図形をしっかり時間をかけて考えられた人は高得点が期待できる内容でした。

一方、数学が苦手な人は、大問1、2、そして各大問の(1)を確実に拾い集めることを優先しましょう。本番では面倒な計算などが要求される(3)は思い切って飛ばす勇気も必要となります。

全体的な難易度　標準

問題の解説

それでは、各大問ごとに詳しく見ていきましょう。

大問1・小問集合

難易度　易

(1)は基本計算です。確実に得点したいところですが、エ、オあたりの計算でも近年は正答率が50％を切ることが増えてきました。

エの計算は通分する際に符号の取り扱いに十分気をつけましょう。オの $\sqrt{50} - \sqrt{32} + \dfrac{\sqrt{6}}{\sqrt{3}}$ は、暗算で

$$5\sqrt{2} - 4\sqrt{2} + \sqrt{2} = 2\sqrt{2}$$

と見て手早く処理しましょう。

(2)は解の公式を使う2次方程式です。公式を適用するだけの何も面白くない問題です。こうした問題で落とすのはバカらしいのできっちり得点しましょう。

(3)は関数の変化の割合です。$y=x^2$ において、$x$ が $a$ から $a+2$ まで変化するとき、変化の割合は

$$\frac{(a+2)^2 - a^2}{(a+2) - a} = \frac{4a+4}{2} = 2a+2$$

これが $y=-2x+7$ の変化の割合 $-2$ と等しいので、

$$2a+2 = -2$$

これを解いて $a = -2$ です。

塾長

例の公式 $a(p+q)$ を知っていると一瞬です。また、変化の割合＝直線の傾き、というイメージを持っていれば計算なしで立式できます。このスピード感が大事です！

(4)は円周角の定理です。$\stackrel{\frown}{\mathrm{BC}}$ に対する円周角が $12^\circ$。$\stackrel{\frown}{\mathrm{AB}}:\stackrel{\frown}{\mathrm{BC}}=3:1$ なので、$\stackrel{\frown}{\mathrm{AB}}$ に対する円周角は $\stackrel{\frown}{\mathrm{BC}}$ の3倍の $36^\circ$ になります。よって中心角は

$$\angle\mathrm{AOB} = 36^\circ \times 2 = 72^\circ$$

$\triangle\mathrm{AOB}$ が二等辺三角形であることに着目して、

$$\frac{180^\circ-72^\circ}{2}=54^\circ$$

となります。

塾長

先を読めていれば、$90-36=54$ と計算して時間を節約できますね！

(5)は確率です。$\dfrac{3a}{2b}$ が整数になる条件を考えます。約分後の分母が1になれば良いので、

• $b=1$ のとき：$\dfrac{3a}{2}$ が整数 $\rightarrow a$ は偶数（2, 4, 6）の3通り
• $b=2$ のとき：$\dfrac{3a}{4}$ が整数 $\rightarrow a$ は4の倍数（4）の1通り
• $b=3$ のとき：$\dfrac{a}{2}$ が整数 $\rightarrow a$ は偶数（2, 4, 6）の3通り
• $b=6$ のとき：$\dfrac{a}{4}$ が整数 $\rightarrow a$ は4の倍数（4）の1通り

これらを合計して8通り。確率は $\dfrac{8}{36} = \dfrac{2}{9}$ です。

大問2・データの活用

難易度　易

大問2はデータの活用（統計）の問題でした。表やグラフがあるため、見た瞬間に「重そうな問題」だと思った人もいたかもしれませんが、内容は非常に浅い問題でした。見た目に惑わされてはいけませんよ。

(1)は表の穴埋めです。

$a$ は度数なので、$200\times 0.20 = 40$。

$b$ は累積相対度数です。B中学校の $30 \sim 40$ の相対度数は表から $0.26$。

これに一つ前までの累積相対度数 $0.22$ を足して、$0.22 + 0.26 = 0.48$ となります。

塾長

模範解答は累積相対度数を使わずにわざわざ相対度数を足していますが、面倒な計算をすれば計算ミスの原因となるので、無駄な計算はやめましょう。

(2)はグラフの読み取り記述です。

グラフを見ると、A中学校の山（ピーク）は20分〜30分のあたりにありますが、B中学校の山は40分〜50分のあたりにあり、全体的に右側に寄っています。

よって、記号は イ（A中学校の方が短い傾向）。

理由は「A中学校のグラフの山が、B中学校よりも左側（時間が短い方）にあるから」といった内容が書けていれば正解です。

塾長

「右にある」「左にある」だけでなく、「通学時間が長い方（短い方）に分布している」と言葉を補足すると、より丁寧な記述になります。

大問3・関数

難易度　易

大問3はダイヤグラム（1次関数）の定番の問題でした。そろそろ余裕をもって解けるようになっておきたい問題です。

(1)はグラフの読み取りです。

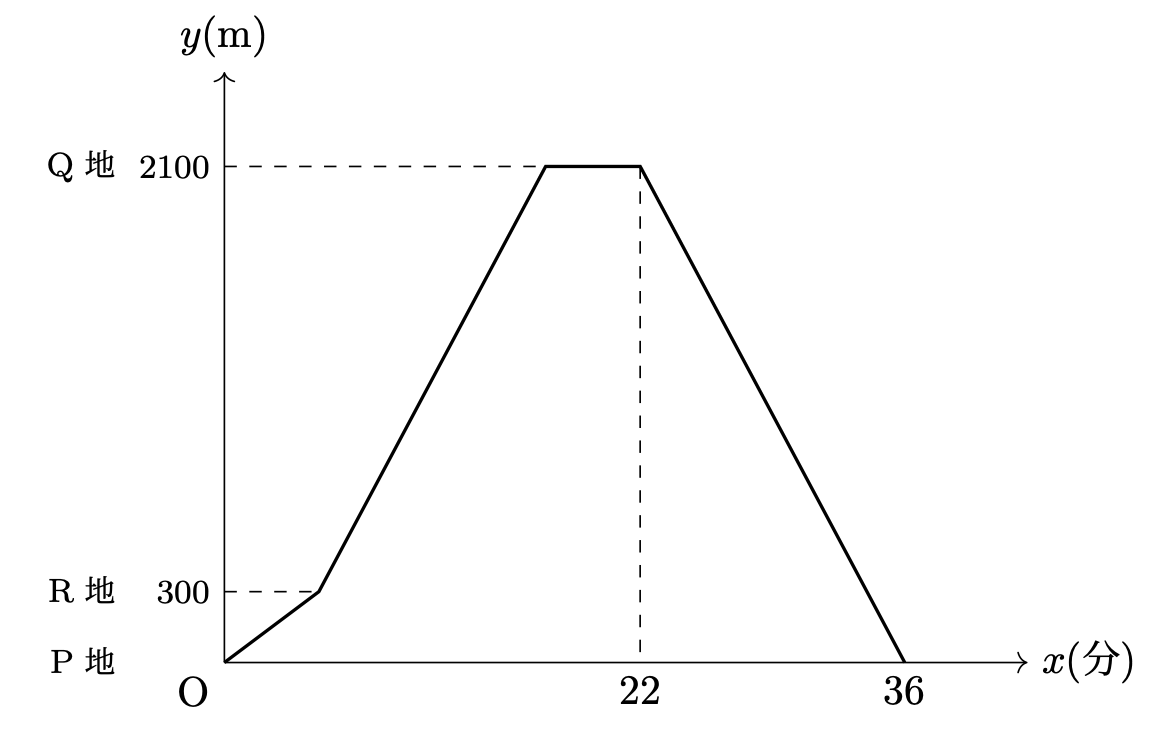
中途半端なグラフなので、問題文からサクッと大事な座標は出しておきたいですね。R地まで分速60mで進んでいるので、300m進むのに5分かかります。さらに、RからQまでは分速150mで、1800m進むことになるので、12分かかります。つまりQ地点についたときは最初から17分後となります。

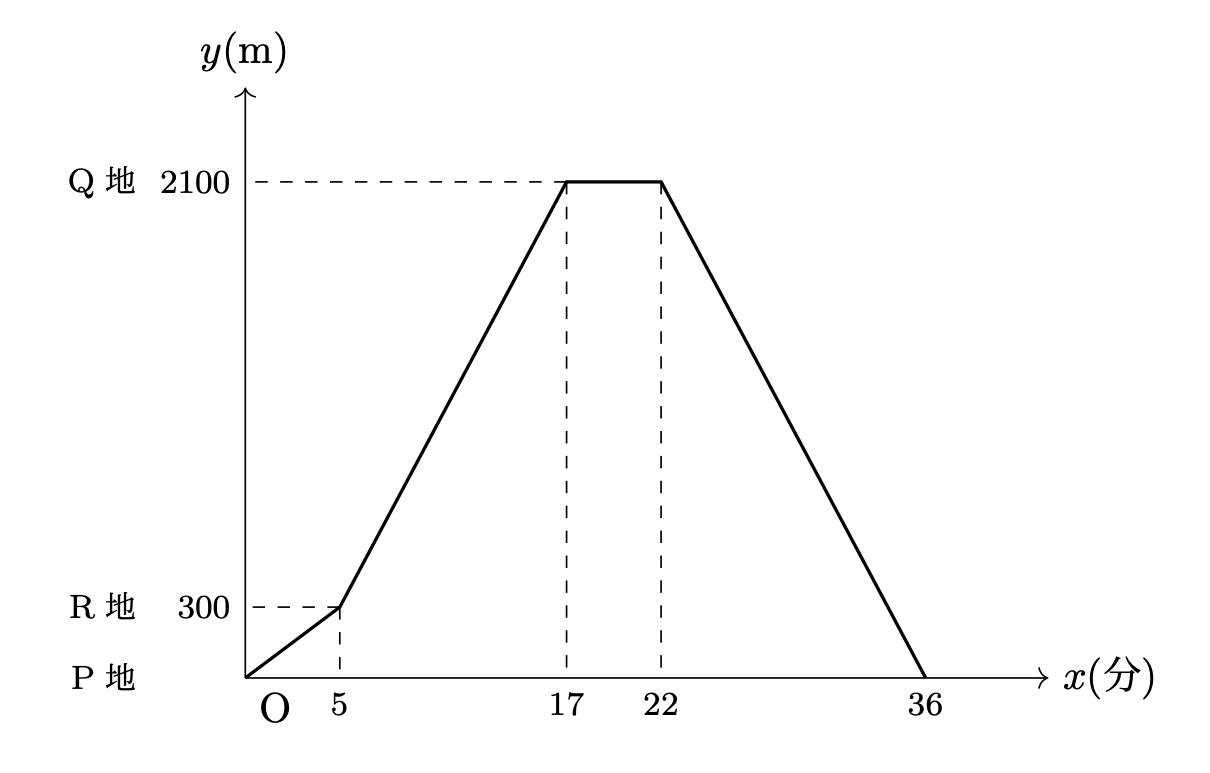
距離が変わっていない水平な部分が休憩時間です。

$$22 - 17 = 5$$

(2)は復路の直線の式です。14分で2100m進む（戻る）ので、傾きは $-\dfrac{2100}{14}=-150$ です。

あとは $y=-150x$ が $(36,\ 0)$ を通るように調節して、$y = -150x + 5400$ となります。

(3)も定番のグラフの追加の問題です。

模範解答にもあるように、グラフの方程式を求めて、それらを連立して解くのが一般的でしょう。

ただ、これだととても面倒に感じるのでもう私はもう少し直感的に解きます。

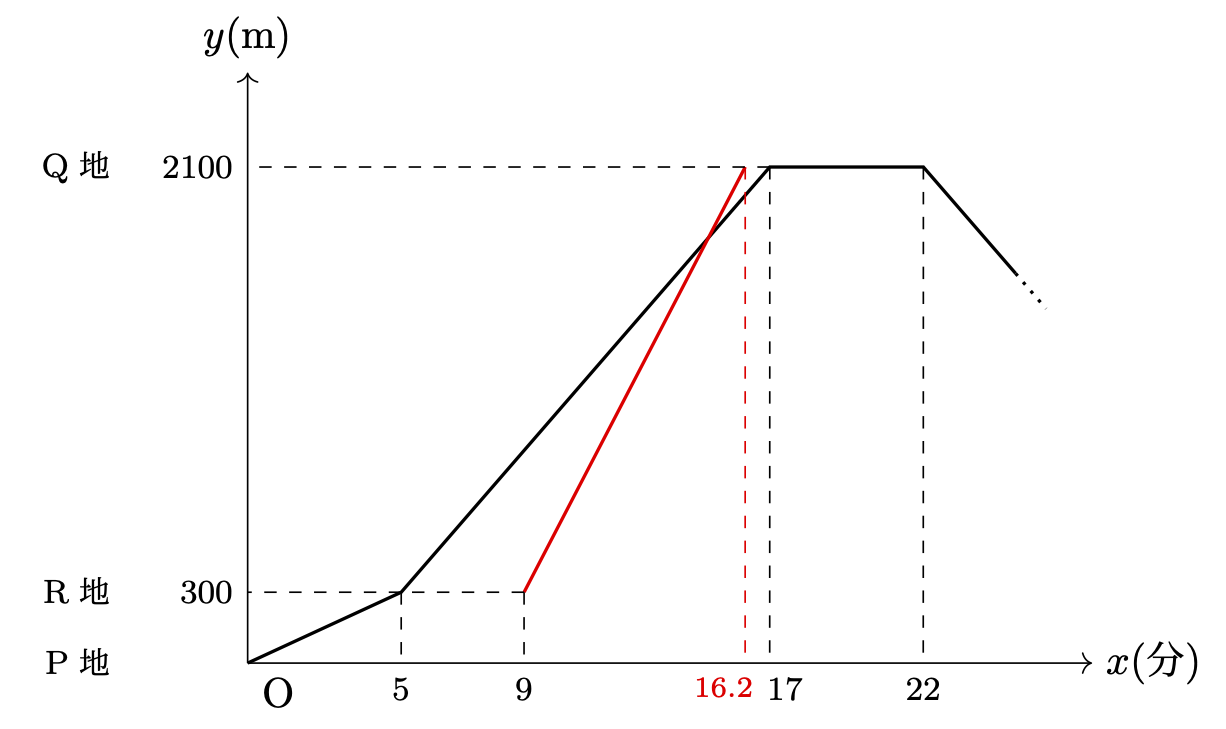
Bさんの動きをグラフに追加すると、赤線のようになります。そのとき、出発点と到着点の $x$ 座標をサクッと出しておきます。そこから、図形的に考えていきましょう。

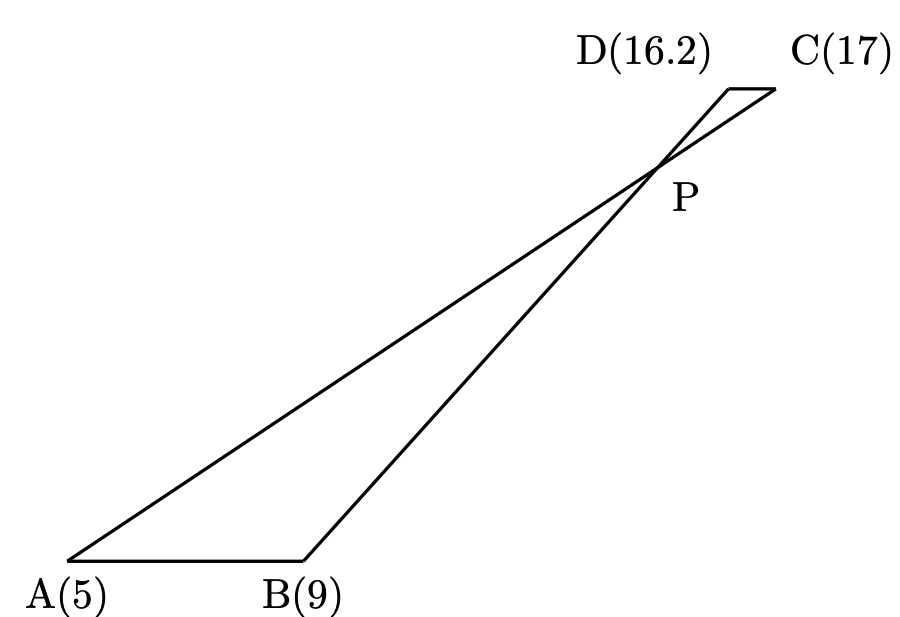
図のようにR地点からQ地点までのAさんとBさんのグラフを取り出して相似な三角形を考えます。相似比は

$$\mathrm{AB:CD=4:0.8=5:1$$

となるので、$1800\times\dfrac{5}{6}=1500$。よって、$1500+300=1800$ と計算しました。

大問4・連立方程式

難易度　易

大問4はシンプルな連立方程式の問題でした。

$$350x+600(60-x)=450\times 60$$

から一発で解けます。$x=36$ となるので、ウォーキング36分、水泳24分です。

大問5・作図

難易度　標準

作図は少し捻りがある問題でしたが、この時期であれば余裕で解いてほしい問題です。

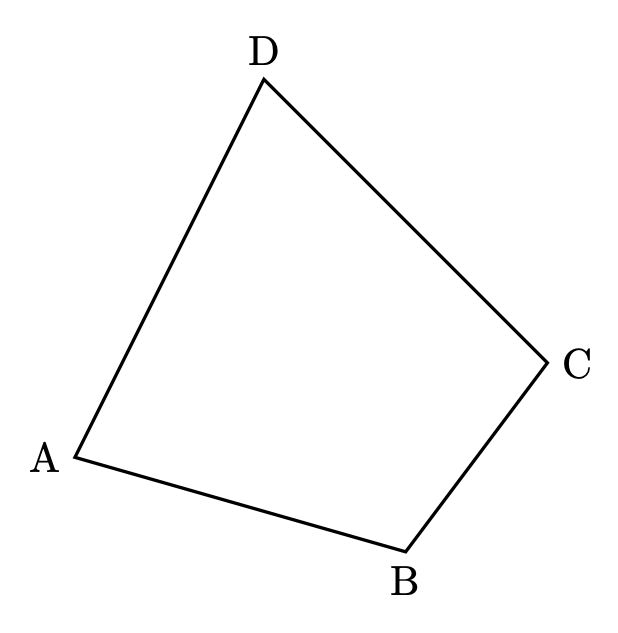
条件①「点Pは辺AB上」はそのまま。

条件②「$\angle \mathrm{CPD} = \angle \mathrm{CAD}$」が最大のヒントです。

2点C, Dを見込む角が等しいということは、4点A, P, C, Dは同一円周上にあるということです。

つまり、求める点Pは「3点A, C, Dを通る円」と「辺AB」との交点になります。

作図の手順は以下の通りです。

1. 線分ADの垂直二等分線を引く。
2. 線分CDの垂直二等分線を引く。
3. その交点Oが外接円の中心になる。
4. Oを中心として、点Aを通る円を描く。
5. 円と辺ABとの交点がP。

大問6・平面図形

難易度　やや難

平面図形の問題は、(3)に苦戦した人が多かったと思います。(1)、(2)は教科書レベルなので落とせない問題です。

(1)は面積です。

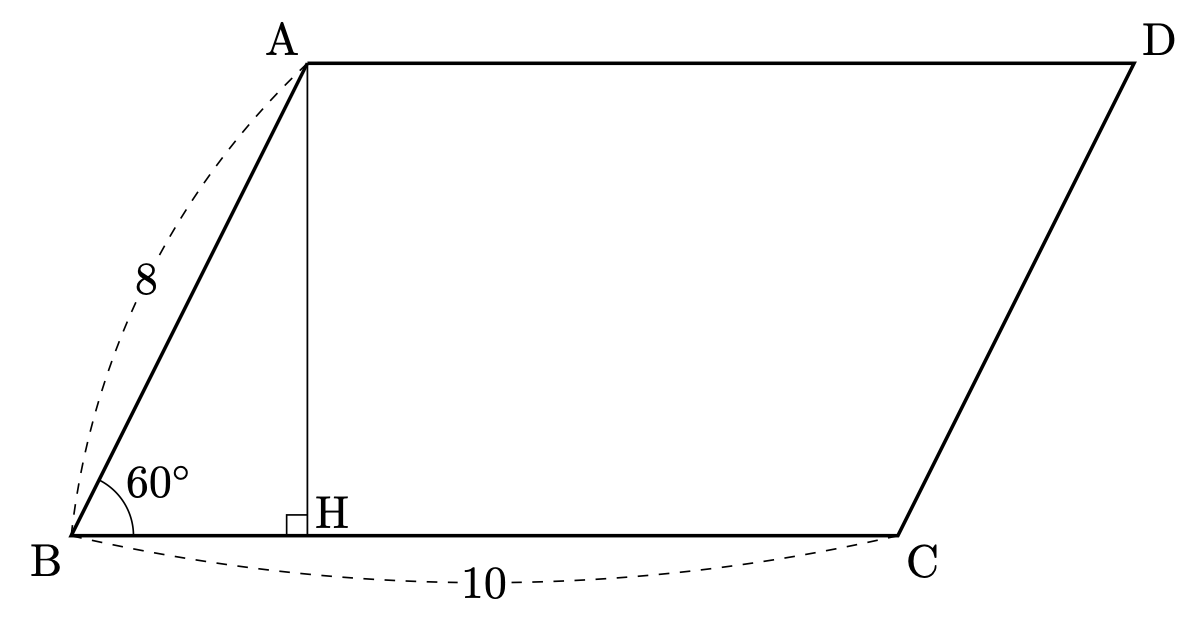
$\mathrm{A}$ から $\mathrm{BC}$ に垂線 $\mathrm{AH}$ を下ろすと、$\angle \mathrm{HBA}=60^\circ$ なので $\triangle\mathrm{ABH}$ は $1:2:\sqrt{3}$ の直角三角形になります。

$\mathrm{AH} = 8 \times \dfrac{\sqrt{3}}{2} = 4\sqrt{3}$ となるので、面積は

$$10 \times 4\sqrt{3} = 40\sqrt{3}$$

(2)は相似の証明でした。

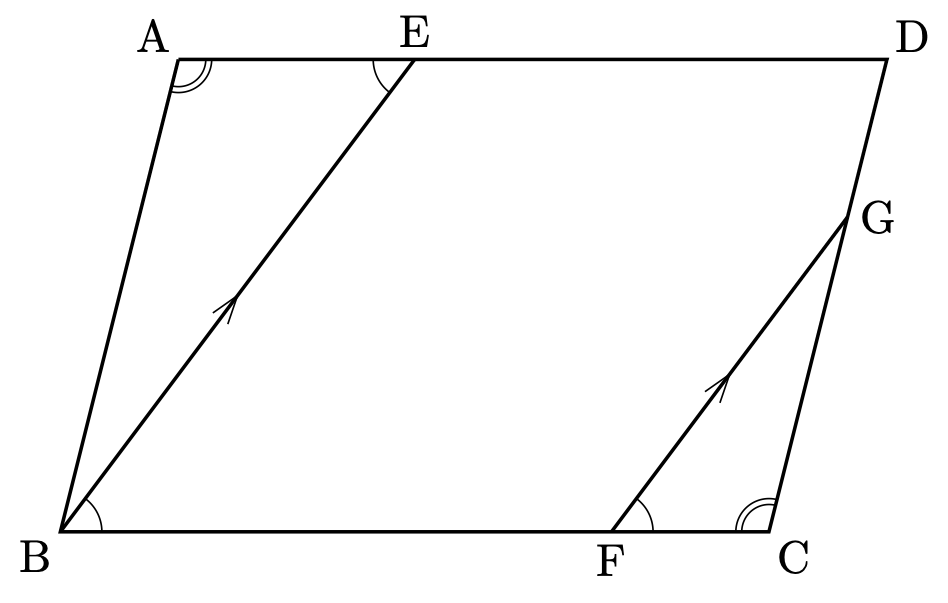
平行四辺形の対角より $\angle \mathrm{BAE} = \angle \mathrm{GCF}$。

平行線の錯角より $\angle \mathrm{AEB} = \angle \mathrm{EBC}$。

平行線の同位角より $\angle \mathrm{EBC} = \angle \mathrm{GFC}$。

よって $\angle \mathrm{AEB} = \angle \mathrm{GFC}$。

2組の角が等しいので相似が証明できました。教科書レベルの基本的な証明ですね。

(3)は難所です。

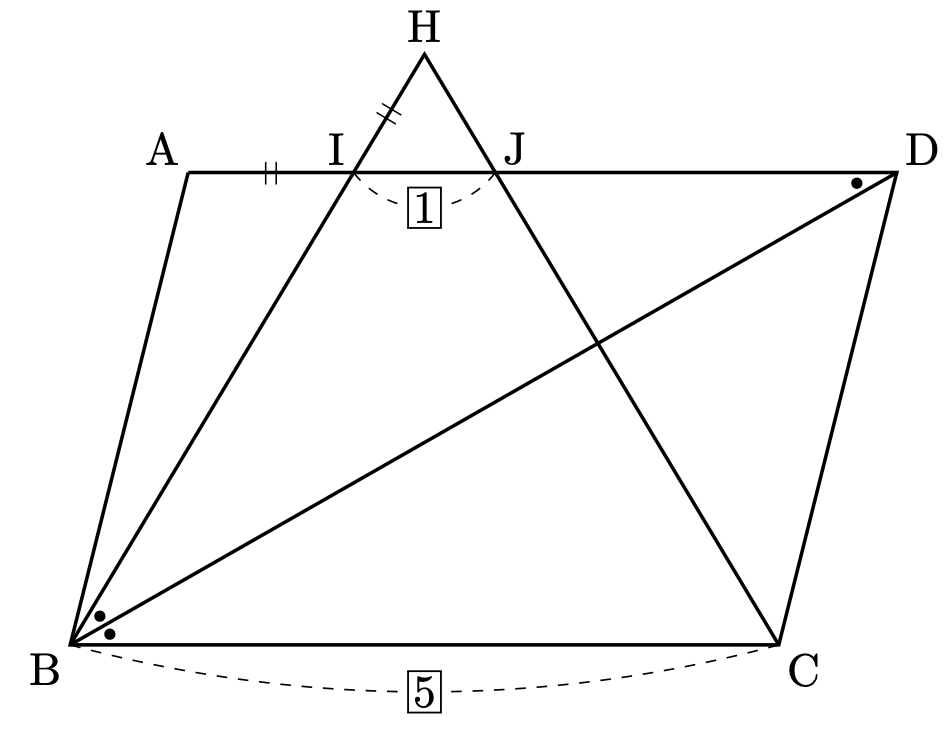
条件より $\triangle \mathrm{IBD}$ が二等辺三角形になり、$\mathrm{IB=ID}$ となることに気づけるかが第一関門です。

さらに $\triangle \mathrm{HIJ} \sim \triangle \mathrm{HBC}$（相似比1:5）と $\mathrm{AI=HI}$ を組み合わせます。少し複雑ですが、$\mathrm{I}$ が $\mathrm{AD}$ を $1:4$ に内分する点となります。$\mathrm{HI:IB=1:4}$ であり、$\mathrm{IB=ID}$、$\mathrm{AI=HI}$ から $\mathrm{AI:ID}=1:4$ が得られます。$\mathrm{AD}$ 上と $\mathrm{BC}$ 上の分割数が揃っていることに注意して、

$$\mathrm{BC} : \mathrm{DJ} = 5 : 3$$

が求められます。ここは差がつく問題でした。

塾長

図形の難問は、わかっている長さや角度からさらに引き出せる情報はないかをよく考えてみることが大切です。与えられた条件を1、2歩踏み込んで考える癖をつけておきましょう。

大問7・空間図形

難易度　難

(1)から少しいつもと違う雰囲気を感じた人が多かったでしょう。どの問題も冷静に考えると大した問題ではないのですが、時間が厳しい中で考えることを想定すると、なかなか難しい問題だったのではないかと思います。

(1)は展開図の問題です。問題というよりはクイズ的な問題で、算数でよく見かける問題でした。組み立てると辺ABに垂直な面は、アとウになります。間違えた人は、問題用紙を切り取って実際に組み立ててみると良いでしょう。

塾長

イメージできるかどうかが大事です。

(2)は回転体の体積を求める問題でした。回転体はたまに出題されるのですが、思考力が弱い人は苦手にしている問題です。今回も、簡単な問題でしたが正答率は低そうです。

$\triangle \mathrm{AFG}$ を軸 $\mathrm{DG}$ 周りに回転させると、外側は円柱、内側は円錐がくり抜かれた形になります。

底面半径は $6$、高さは $6\sqrt{2}$ です。

$$V = \pi \cdot 6^2 \cdot 6\sqrt{2} \times \frac{2}{3} = 144\sqrt{2}\pi$$

塾長

この計算をするときにわざわざ「円柱から円錐を引く」という操作をしている人は、公式を覚えて使っているだけの人の可能性大です。やっていることは間違っていませんが、理解できているとは言えません。気をつけましょう。

(3)は線分の長さを求める問題でした。かなり面倒な問題でしたが、やること自体はシンプルです。分けて考える、それだけの話です。

鍵となるのは点 $\mathrm{J}$ の位置です。これを考えるために、まずは下のような図（平面 $\mathrm{AFI}$）を考えます。

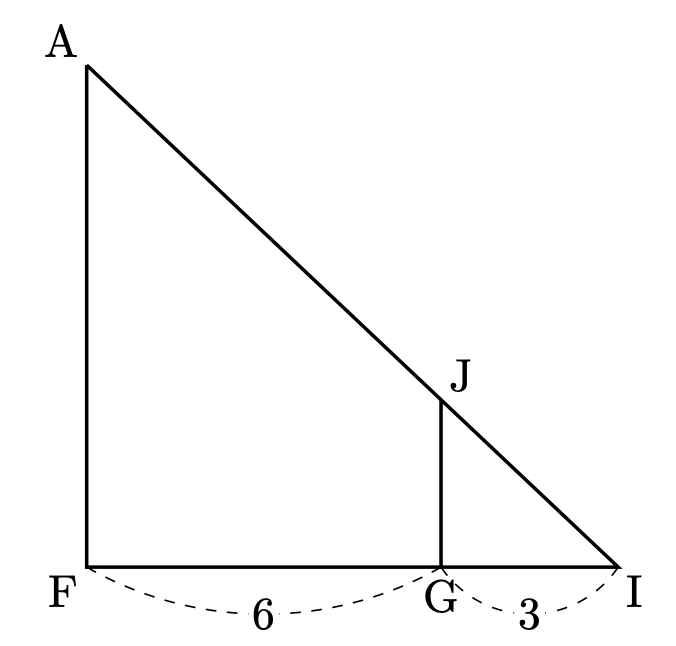
図から、$\mathrm{AJ} : \mathrm{AI} = 6 : 9 = 2 : 3$

つまり、点 $\mathrm{J}$ は、線分 $\mathrm{AI}$ を $2:1$ に内分する位置にあります。

線分 $\mathrm{AI}$ 上で「$\mathrm{A}$ から $2/3$ 進んだ場所」が $\mathrm{J}$ ということなので、これを「高さ」と「奥行き」に分けて考えます。

高さ（上下）の変化

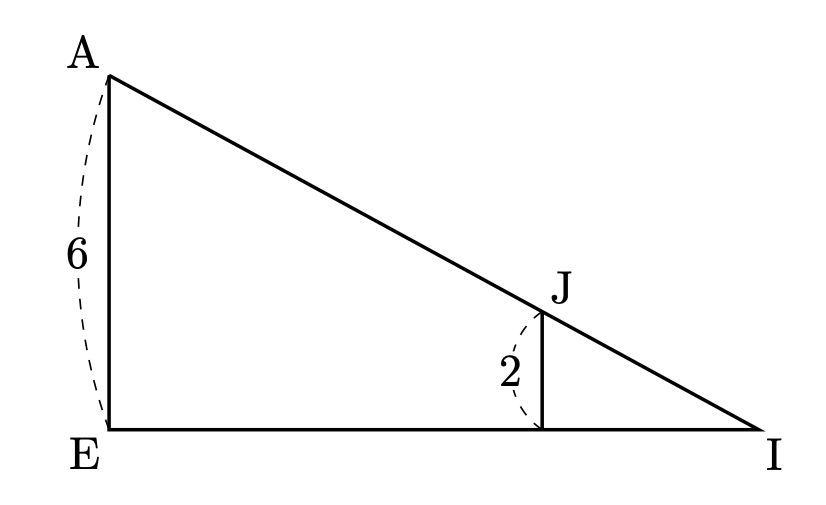
$\mathrm{A}$ の高さ $6$、$\mathrm{I}$の高さ $0$ であり、$\mathrm{A}$ から $\mathrm{I}$ に向かって $\dfrac{2}{3}$ 進むので、高さも $\dfrac{2}{3}$ 下がります。したがって、$\mathrm{J}$ は、底面から $2$ だけ上の高さにあります。

奥行き（前後）の変化（真上から見た図を考えます）

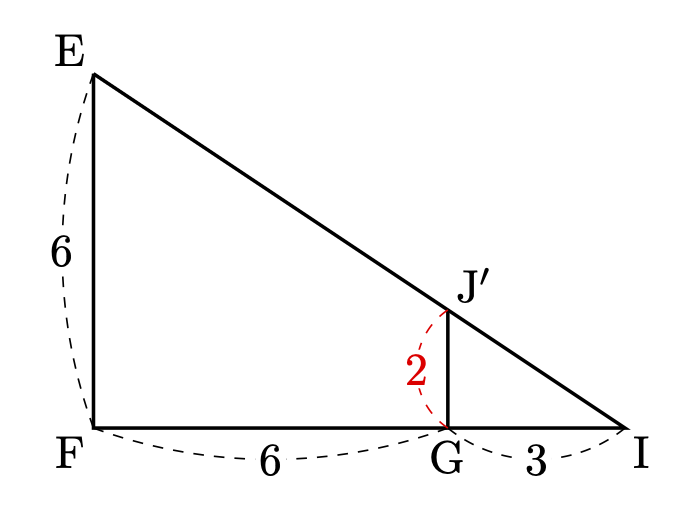
$\mathrm{J}$ を平面 $\mathrm{EFGH}$ に投影した点を $\mathrm{J}'$ としています。$\mathrm{A}$ の位置は手前の面から6だけ奥にあり、$\mathrm{I}$ は $0$ となります。つまり$\mathrm{A}$ から手前に向かって $\dfrac{2}{3}$ 進みます、したがって、$\mathrm{J}$ の位置は手前の面から $2$ の位置にあります。

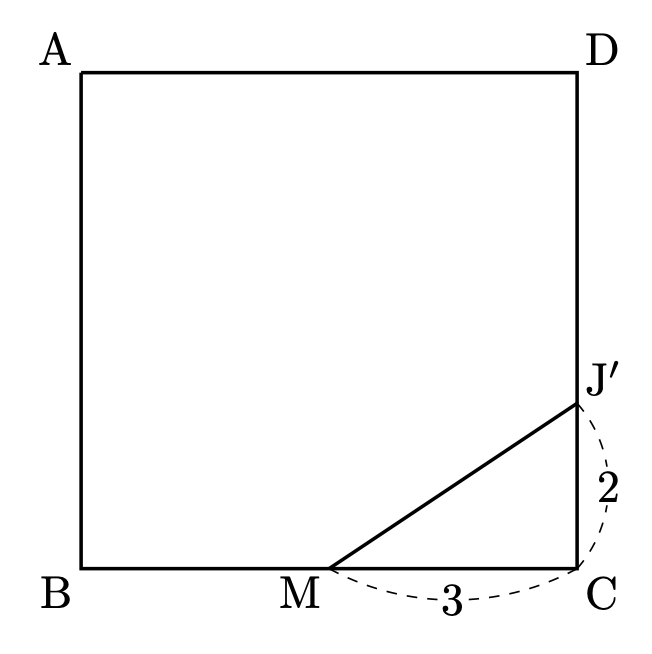
再度真上から見た図を考えます。$\mathrm{M}$ を通って平面 $\mathrm{ABCD}$ に平行な面に $\mathrm{J}$ を投影した点を $\mathrm{J}'$ とします。このとき、三平方の定理から

$$\mathrm{MJ}'=\sqrt{3^2+2^2}=\sqrt{13}$$

となります。次に、$\triangle\mathrm{MJJ}'$ を考えます。

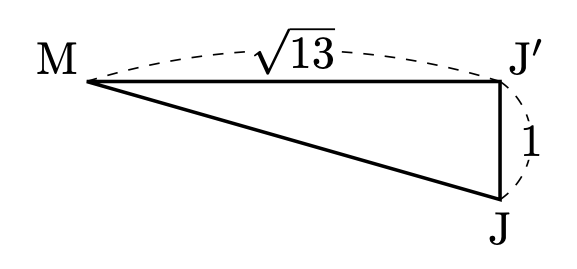
$\mathrm{M}$ と $\mathrm{J}$ の底面からの高さの差は 3-2=1$ に注意して三平方の定理を用いると

$$\mathrm{MJ}=\sqrt{(\sqrt{13})^2+1^2}=\sqrt{14}$$

となります。

塾長

視点をいといろと動かしながら考える必要があるので、苦手な人はとことん苦手な問題だったと思います。この手の問題が差がつきやすいので、得意な人はきっちり解き切っておきたいところです。

まとめ

今回の模試は、前半の基本問題での失点を防ぎつつ、後半の応用問題（特に大問6(3)や大問7(3)）にどれだけ食らいつけたかがポイントでした。

時間が足りなかった人は、「どの問題は見送って、どの問題に時間をかけるか」という判断基準をもう一度見直しておきましょう。

私立高校入試も終わり、あとは国立と公立高校入試に向けて集中する時期です。

解説を読んで「なるほど！」で終わらせず、「自力で解けるようになるまで」復習を徹底しましょう。それが合格への最短ルートです。

塾長

インフルエンザが猛威をふるっていますが体調管理も受験勉強のうちです。無理しすぎず、でも自分を甘やかさず。最後まで頑張っていきましょう！