3次曲線の対称性

本日の高3生は微積分の応用問題(方程式・面積)をやった。
とくに面積関係では3次曲線について、どこまで理解しているかが重要だと思っている。
今日の授業では3次関数の対称性を利用する(と簡単になる)問題を扱ったのだが、対称性をもつことさえ知らない生徒が多くで驚いた。というのは嘘で、もうこのくらいのことでは驚かない。そうだろうな、くらいの感覚である。
教科書には載っていないわけだが、導関数を学ぶのだからこのくらいは知っておいて欲しい部分である。
3次関数を微分すると2次関数が得られる。このとき、微分して得られる2次関数のグラフは放物線であり、対称軸をもつ。したがって、3次関数のグラフも対称の中心をもつだろうと考えられるようになって欲しい。
微分して得られる2次関数のグラフの性質を最大限に活用していくことが3次関数の問題を素早く解くコツでもある。
とくにセンター試験などでは、知っているか知らないかで計算の負担がかなり異なる。
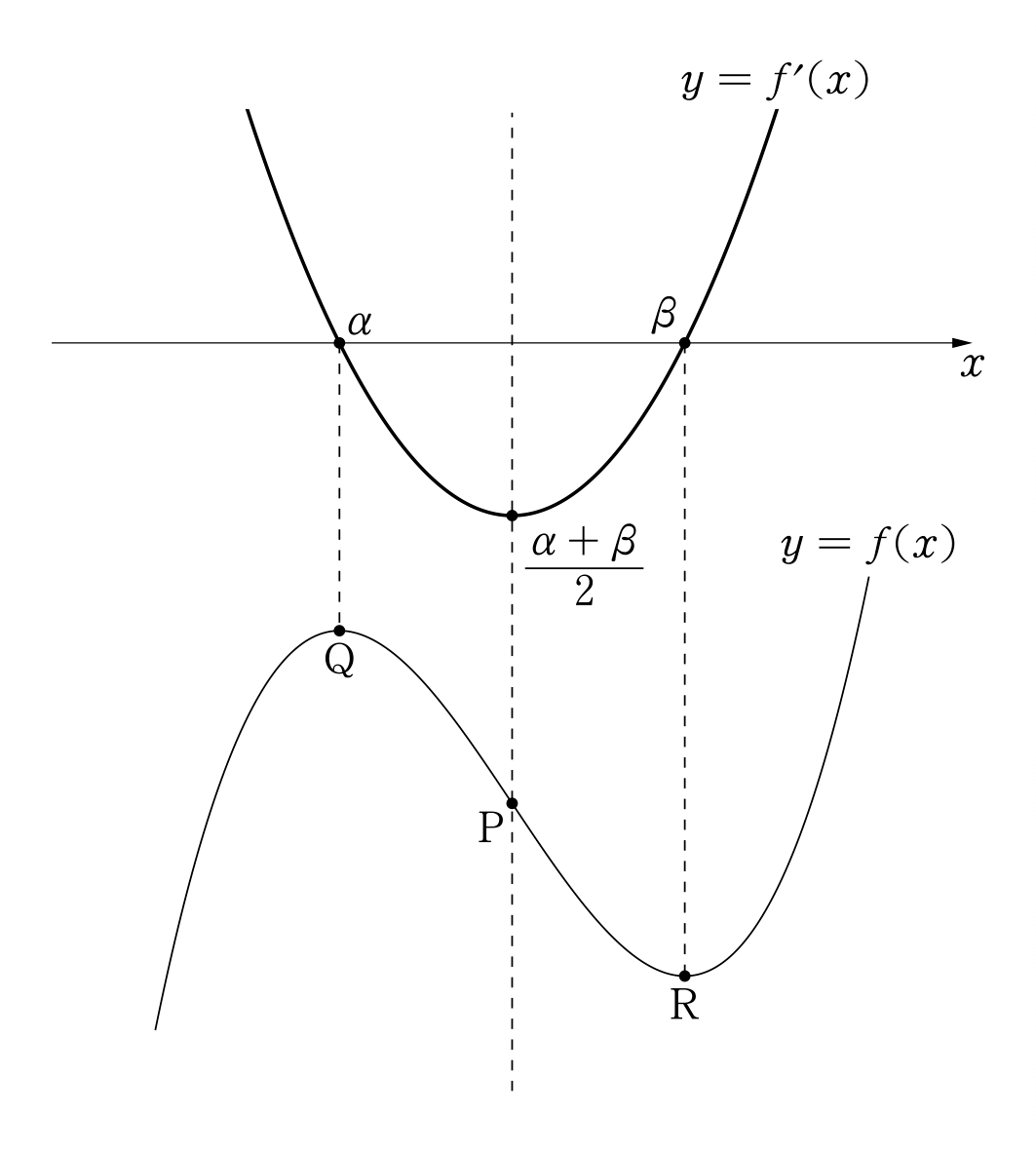
重要なのは、微分して得られる2次関数が異なる2実解をもつような下図のパターンだろう。
図のPが3次曲線の対称の中心となる「変曲点」となる。そしてQ、Rが極値となる。
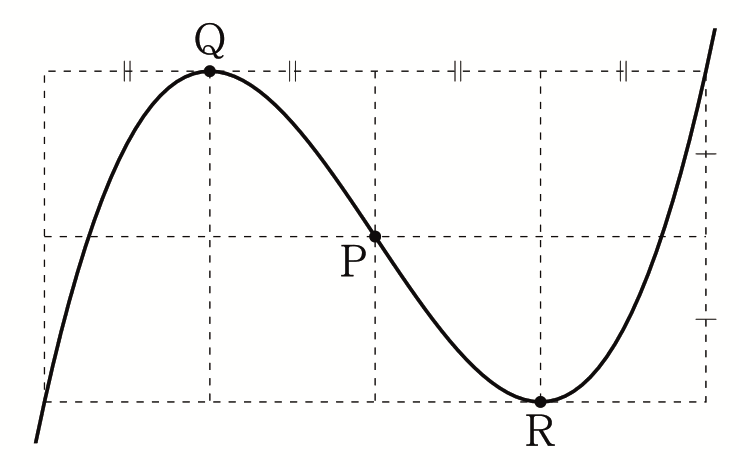
この対応は3次曲線を学ぶのであれば知っておきたい性質だ。さらに、3次関数のグラフは、2つの極値および変曲点を用いて次の図のように8等分されることは確認しておきたい。
せっかく微積分を学ぶのに、導関数を調べることの意味がよく分かっていない人が多い。
単純に $f'(x)=0$ だけを計算して増減表を書くくらいのものにしか思っていない生徒が多すぎる印象である。
こういう話は、積分についても同じで、$\displaystyle \frac{1}{6}$ 公式を使っているにもかかわらず、放物線の面積の比のことは何も知らないという生徒もいた。
おそらく、そうした「公式」を教わって、何も考えずにただ使ってきたんだろうなあと思う。
それでは数学をやっている意味なんてほとんどなくて、単にテストの点を取る方法を一生懸命にやっているだけである。当然ながら実力はつかないだろうし、2次試験のレベルあたりになると相当苦労するだろう。
そう伝えても生徒本人は実感が持てないようで、「いや、できてるから」なんて思われてしまうのがまた恐ろしいけど。
ちなみに、数学ができる生徒は、こうしたことを教わっても、それを使うことで満足せず必ず自分で確認したりする習慣があるように思う。俺もそうだったけど。鵜呑みにするということをあまりやらない(そのせいで性格悪いとか言われるけど心外だなあ)。
ただ、3次曲線の対称性については、結構点数に直結するような話だから、食いつきがいい。
でも、点数になるかどうかという判断基準ではなく、面白いかどうかという判断基準を持てるようになってもらいたい。遠回りになるかもしれないが、そうした面白い部分を深めていくことが、最終的には実力を大きく上げてくれるのである。塾生たちを見ていると、そういうことを強く感じる今日この頃である。
ちなみに放物線の面積比の話は以下の記事でもちょっと触れている。













